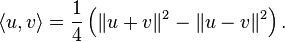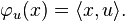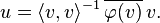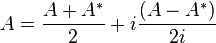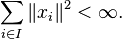Friday, August 19, 2011
Surfing Troves: how to retrieve the info of the compiler having bu...
Surfing Troves: how to retrieve the info of the compiler having bu...: Sometime there happens to be a need for retrieving what is the compilation information, compiler version, say, of the compiler that was prev...
Thursday, July 28, 2011
Surfing Troves: Can not hear from earphone on fedora linux ALSA Co...
Surfing Troves: Can not hear from earphone on fedora linux ALSA Co...: "1. check if the file /etc/modprobe.d/alsa-base exists, touch an empty one of this if not. 2. add following line to it : options snd-hd..."
Surfing Troves: Defeating the MesaLib installation issues - not su...
Surfing Troves: Defeating the MesaLib installation issues - not su...: "While obstructed by the tricky installation of GLUT-3.7 in Linux (Fedora 13/14 in this post's case), an easy expedient is to indirectly ins..."
Surfing Troves: Tracing the segmentation fault problem caused by g...
Surfing Troves: Tracing the segmentation fault problem caused by g...: "When porting an openGL+freeGLUT program to a laptop running with an integrated on-board graphics card ( actually, a part of the chipset, th..."
Friday, June 17, 2011
Surfing Troves: Q&A for Oracle Distributed Database Application De...
Surfing Troves: Q&A for Oracle Distributed Database Application De...: "1. Driver installation – oracle JDBC Like the installation of JDBC driver for MySql , installing the JDBC driver for oracle also needs to ..."
Surfing Troves: Easy way to bakup/copy MBR under linux
Surfing Troves: Easy way to bakup/copy MBR under linux: "1. get to know where the current MBR lies sudo /sbin/fdisk -l the line tagged with an asterisk in between (aligned with column 'Boot' ) i..."
Surfing Troves: Running an existing OS in VirtualBox under Fedora ...
Surfing Troves: Running an existing OS in VirtualBox under Fedora ...: "(Copied precisely from http://blog.amhill.net/2010/01/27/linux-ftw-using-virtualbox-with-an-existing-windows-partition/ ) Install Virtual B..."
Surfing Troves: Compiling Openmotif under Fedora 13 - error: X11/b...
Surfing Troves: Compiling Openmotif under Fedora 13 - error: X11/b...: "Stumped with the nag for long when I was compiling OpenMotif 2.3.3 Download package at : http://www.motifzone.net/files/public_downloads/..."
Surfing Troves: Building installation of FreeWRL for Fedora 12/13/...
Surfing Troves: Building installation of FreeWRL for Fedora 12/13/...: "The official site of FreeWRL only provides installation guide for Ubuntu in the range of Linux series. While different OS has different too..."
Surfing Troves: Compiling OpenVRML - error : cannot find -lltdl
Surfing Troves: Compiling OpenVRML - error : cannot find -lltdl: "This is because of loss of the static library libltdl.a, which is one of the output if you install libtool To make up, simply download the..."
Surfing Troves: Linux / Fedora 64 - upgraded package and library n...
Surfing Troves: Linux / Fedora 64 - upgraded package and library n...: "while upgrading GTK+ by building the package from the source code from http://www.gtk.org/download-linux.html , following the simplest step..."
Surfing Troves: Acrobat reader 9.0 failed to load libraries in the...
Surfing Troves: Acrobat reader 9.0 failed to load libraries in the...: "Having run into the nasty problem with acrobat reader in the Linux (Fedora 13 64bit): /opt/Adobe/Reader9/Reader/intellinux/bin/acroread: e..."
Surfing Troves: Can not find the atk library or version is lower t...
Surfing Troves: Can not find the atk library or version is lower t...: "Yet another prerequisite for GTK+, which might be complaining the lower version than required or simply loss of it: 1. retrieve package pe..."
Surfing Troves: Can not find the pango library or version is lower...
Surfing Troves: Can not find the pango library or version is lower...: "Another prerequisite for GTK+, which might be complaining the lower version than required or simply loss of it: 1. check the current ver..."
Surfing Troves: Can not find the cairo library or version is lower...
Surfing Troves: Can not find the cairo library or version is lower...: "One more prerequisite for GTK+, which might be complaining the lower version than required or simply loss of it: try to reinstall in th..."
Surfing Troves: Can not find the gdk-pixbuf library or version is ...
Surfing Troves: Can not find the gdk-pixbuf library or version is ...: "One more, maybe last in the nasty complaining list for building GTK+-2.22.1, prerequisite for GTK+, which might be complaining the lower ver..."
Surfing Troves: Ordeal with Installation of GTK+-2.4 in Linux Env...
Surfing Troves: Ordeal with Installation of GTK+-2.4 in Linux Env...: "1. go ftp://ftp.gtk.org/pub/gtk/v2.4/ : wget ftp://ftp.gtk.org/pub/gtk/v2.4/glib-2.4.7.tar.bz2 bunzip glib-2.4.7.tar.bz2 && tar xvf ..."
Surfing Troves: Surfing Troves: Can not find the atk library or ve...
Surfing Troves: Surfing Troves: Can not find the atk library or ve...: "Surfing Troves: Can not find the atk library or version is lower t... : 'Yet another prerequisite for GTK+, which might be complaining the l..."
Surfing Troves: Surfing Troves: Can not find the cairo library or ...
Surfing Troves: Surfing Troves: Can not find the cairo library or ...: "Surfing Troves: Can not find the cairo library or version is lower... : 'One more prerequisite for GTK+, which might be complaining the lowe..."
Surfing Troves: Linux : Access network service in Single user mod...
Surfing Troves: Linux : Access network service in Single user mod...: "1. Enter the Level 1 - Single User Mode In the grub boot memu, select the entry for the OS you want to start up, press 'e' to edit : Just ..."
Surfing Troves: Fedora Linux : Always got wrong IP configured
Surfing Troves: Fedora Linux : Always got wrong IP configured: "while the network configuration in the ifcfg-eth0 is as follows: IPADDR=x.x.31.231 BROADCAST=x.255.255.255 NETWORK=x.x.31.0 NETMASK=255..."
Surfing Troves: Nvidia driver problems in Fedora Linux X86_64 - ch...
Surfing Troves: Nvidia driver problems in Fedora Linux X86_64 - ch...: "1. for the first issue, however reinstalling the driver, updating by nvidia-installer -a --update (internet access should be firstly ready)..."
Surfing Troves: Fedora Linux : can not see any icon on the deskto...
Surfing Troves: Fedora Linux : can not see any icon on the deskto...: "This is simply because nautilus (Fedora file explorer/manager) failed to create the 'Desktop' directory under $HOME of current the login use..."
Surfing Troves: Surfing Troves: Q&A for Oracle Distributed Databas...
Surfing Troves: Surfing Troves: Q&A for Oracle Distributed Databas...: "Surfing Troves: Q&A for Oracle Distributed Database Application De... : 'p { margin-bottom: 0.08in; }h2 { margin-bottom: 0.08in; }h2.western..."
Surfing Troves: How to copy all including hidden files or director...
Surfing Troves: How to copy all including hidden files or director...: "While copying all stuff under a directory into another place, by cp $SRC/* $DST will fail to copy all the hidden file (prefixing with ..."
Surfing Troves: How to restore or upgrade Fedora linux without los...
Surfing Troves: How to restore or upgrade Fedora linux without los...: "When you are inflicted with some faults of current Linux, the Fedora distribution, say, you might want to restore the OS kernel only withou..."
Surfing Troves: Restore Linux installation after installing Window...
Surfing Troves: Restore Linux installation after installing Window...: "By default Linux uses the grub Bootloader to manage OS booting with support of multiple OS, and this makes Linux, Fedora distribution say, r..."
Surfing Troves: uninterruptedly running program in the background ...
Surfing Troves: uninterruptedly running program in the background ...: "For instance, wanna copy a big file, more than 10G, say, from remote host to local machine by a shell like : scp -r user@hostname/ip:/h..."
Surfing Troves: Surfing Troves: Building installation of FreeWRL f...
Surfing Troves: Surfing Troves: Building installation of FreeWRL f...: "Surfing Troves: Building installation of FreeWRL for Fedora 12/13/... : 'The official site of FreeWRL only provides installation guide for U..."
Surfing Troves: Install Nvidia Driver (non Gefore series) in Fedor...
Surfing Troves: Install Nvidia Driver (non Gefore series) in Fedor...: "Intro: While here places a complete guide that is already great for novices in Fedora community at http://www.if-not-true-then-false.com/2..."
Surfing Troves: A Funny Time Varying VIM color scheme switching
Surfing Troves: A Funny Time Varying VIM color scheme switching: "Vi/vim is really the most popular editor under Linux esp. for those advanced users or Linux fans, even though there are dozen of other fea..."
Surfing Troves: Fix bugs for Buidling installation of G3D 7.01 in ...
Surfing Troves: Fix bugs for Buidling installation of G3D 7.01 in ...: "Today I am porting such and such a project which is dependent on G3D and for historical reasons this project could not work with other vers..."
Surfing Troves: Can not find man page for GLUT routines in Linux?
Surfing Troves: Can not find man page for GLUT routines in Linux?: "I made up the man page for GLUT (so that I can ^K to call the API manual out while the cursor is on the words symbolizing GLUT routines) by ..."
Surfing Troves: How to get the screen resolution in Linux C (and m...
Surfing Troves: How to get the screen resolution in Linux C (and m...: "Linux C: get the screen resolution and window size Happened to necessitate the retrieval of information about the screen of the canonica..."
Surfing Troves: Enable X Shared Memory Extension Pixmaps
Surfing Troves: Enable X Shared Memory Extension Pixmaps: "Definitely not encouraged to use, sometimes this feature is needed for using certain applications what depends on this deprecated X window e..."
Surfing Troves: remove empty line by sed or in vim
Surfing Troves: remove empty line by sed or in vim: "In vim, following the same trick for general sustitution: :%s/ ^[\ \t]*\n // g By sed on the command line: cat orgfile | sed /^$/d"
Surfing Troves: Why vim not search STL headers?
Surfing Troves: Why vim not search STL headers?: "In vim it is common to open a header in place, which is really a handy feature for browsing a directory hierarchy. But you might find this..."
Surfing Troves: A TUI library for Dos/Windows
Surfing Troves: A TUI library for Dos/Windows: "A Text User Interface Library in C++ for DOS/Windows. Useful for building light-weighted TUI based applications. http://sourceforge.net/u/..."
Surfing Troves: building installation of freeglut ------ problem w...
Surfing Troves: building installation of freeglut ------ problem w...: "When setting up freeglut with the source code package downloaded from sourceForge in the Fedora Linux environment, there always complains in..."
Surfing Troves: On how universities handle multiple GRE scores (ho...
Surfing Troves: On how universities handle multiple GRE scores (ho...: "RESULTS FROM Google 'more than one gre scores' or ' Multiple GRE scores' (first 50 pages according to the page-rank) ---------------..."
Sunday, April 10, 2011
Hilbert's problems
(excerpted from http://en.wikipedia.org/wiki/Hilbert%27s_problems)
Hilbert's twenty-three problems are:
Hilbert's twenty-three problems are:
| Problem | Brief explanation | Status | Year Solved |
|---|---|---|---|
| 1st | The continuum hypothesis (that is, there is no set whose cardinality is strictly between that of the integers and that of the real numbers) | Proven to be impossible to prove or disprove within the Zermelo–Fraenkel set theory with or without the Axiom of Choice. There is no consensus on whether this is a solution to the problem. | 1963 |
| 2nd | Prove that the axioms of arithmetic are consistent. | There is no consensus on whether results of Gödel and Gentzen give a solution to the problem as stated by Hilbert. Gödel's second incompleteness theorem, proved in 1931, shows that no proof of its consistency can be carried out within arithmetic itself. Gentzen proved in 1936 that the consistency of arithmetic follows from the well-foundedness of the ordinal ε0. | 1936? |
| 3rd | Given any two polyhedra of equal volume, is it always possible to cut the first into finitely many polyhedral pieces which can be reassembled to yield the second? | Resolved. Result: no, proved using Dehn invariants. | 1900 |
| 4th | Construct all metrics where lines are geodesics. | Too vague to be stated resolved or not.[n 1] | – |
| 5th | Are continuous groups automatically differential groups? | Resolved by Andrew Gleason, depending on how the original statement is interpreted. If, however, it is understood as an equivalent of the Hilbert–Smith conjecture, it is still unsolved. | 1953? |
| 6th | Axiomatize all of physics | Unresolved. [n 2] | – |
| 7th | Is a b transcendental, for algebraic a ≠ 0,1 and irrational algebraic b ? | Resolved. Result: yes, illustrated by Gelfond's theorem or the Gelfond–Schneider theorem. | 1935 |
| 8th | The Riemann hypothesis ("the real part of any non-trivial zero of the Riemann zeta function is ½") and other prime number problems, among them Goldbach's conjecture and the twin prime conjecture | Unresolved. | – |
| 9th | Find most general law of the reciprocity theorem in any algebraic number field | Partially resolved.[n 3] | – |
| 10th | Find an algorithm to determine whether a given polynomial Diophantine equation with integer coefficients has an integer solution. | Resolved. Result: impossible, Matiyasevich's theorem implies that there is no such algorithm. | 1970 |
| 11th | Solving quadratic forms with algebraic numerical coefficients. | Partially resolved.[citation needed] | – |
| 12th | Extend the Kronecker–Weber theorem on abelian extensions of the rational numbers to any base number field. | Unresolved. | – |
| 13th | Solve all 7-th degree equations using continuous functions of two parameters. | Resolved. The problem was solved affirmatively by Vladimir Arnold based on work by Andrei Kolmogorov. [n 5] | 1957 |
| 14th | Is the ring of invariants of an algebraic group acting on a polynomial ring always finitely generated? | Resolved. Result: no, counterexample was constructed by Masayoshi Nagata. | 1959 |
| 15th | Rigorous foundation of Schubert's enumerative calculus. | Partially resolved.[citation needed] | – |
| 16th | Describe relative positions of ovals originating from a real algebraic curve and as limit cycles of a polynomial vector field on the plane. | Unresolved. | – |
| 17th | Expression of definite rational function as quotient of sums of squares | Resolved. Result: An upper limit was established for the number of square terms necessary.[citation needed] | 1927 |
| 18th | (a) Is there a polyhedron which admits only an anisohedral tiling in three dimensions? (b) What is the densest sphere packing? | (a) Resolved. Result: yes (by Karl Reinhardt). (b) Resolved by computer-assisted proof. Result: cubic close packing and hexagonal close packing, both of which have a density of approximately 74%.[n 6] | (a) 1928 (b) 1998 |
| 19th | Are the solutions of Lagrangians always analytic? | Resolved. Result: yes, proven by Ennio de Giorgi and, independently and using different methods, by John Forbes Nash. | 1957 |
| 20th | Do all variational problems with certain boundary conditions have solutions? | Resolved. A significant topic of research throughout the 20th century, culminating in solutions[citation needed] for the non-linear case. | – |
| 21st | Proof of the existence of linear differential equations having a prescribed monodromic group | Resolved. Result: Yes or no, depending on more exact formulations of the problem.[citation needed] | – |
| 22nd | Uniformization of analytic relations by means of automorphic functions | Resolved.[citation needed] | – |
| 23rd | Further development of the calculus of variations | Unresolved. | – |
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions. A Hilbert space is an abstract vector space possessing the structure of an inner product that allows length and angle to be measured. Furthermore, Hilbert spaces are required to be complete, a property that stipulates the existence of enough limits in the space to allow the techniques of calculus to be used.
Hilbert spaces arise naturally and frequently in mathematics, physics, and engineering, typically as infinite-dimensional function spaces. The earliest Hilbert spaces were studied from this point of view in the first decade of the 20th century by David Hilbert, Erhard Schmidt, and Frigyes Riesz. They are indispensable tools in the theories of partial differential equations, quantum mechanics, Fourier analysis (which includes applications to signal processing and heat transfer) and ergodic theory which forms the mathematical underpinning of the study of thermodynamics. John von Neumann coined the term "Hilbert space" for the abstract concept underlying many of these diverse applications. The success of Hilbert space methods ushered in a very fruitful era for functional analysis. Apart from the classical Euclidean spaces, examples of Hilbert spaces include spaces of square-integrable functions, spaces of sequences, Sobolev spaces consisting of generalized functions, and Hardy spaces of holomorphic functions.
Geometric intuition plays an important role in many aspects of Hilbert space theory. Exact analogs of the Pythagorean theorem and parallelogram law hold in a Hilbert space. At a deeper level, perpendicular projection onto a subspace (the analog of "dropping the altitude" of a triangle) plays a significant role in optimization problems and other aspects of the theory. An element of a Hilbert space can be uniquely specified by its coordinates with respect to a set of coordinate axes (an orthonormal basis), in analogy with Cartesian coordinates in the plane. When that set of axes is countably infinite, this means that the Hilbert space can also usefully be thought of in terms of infinite sequences that are square-summable. Linear operators on a Hilbert space are likewise fairly concrete objects: in good cases, they are simply transformations that stretch the space by different factors in mutually perpendicular directions in a sense that is made precise by the study of their spectrum.
The norm defined by the inner product 〈•,•〉 is the real-valued function
Relative to a distance function defined in this way, any inner product space is a metric space, and sometimes is known as a pre-Hilbert space.[4] A pre-Hilbert space is a Hilbert space if in addition it is complete. Completeness is expressed using a form of the Cauchy criterion for sequences in H: a pre-Hilbert space H is complete if every Cauchy sequence converges with respect to this norm to an element in the space. Completeness can be characterized by the following equivalent condition: if a series of vectors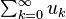 converges absolutely in the sense that
converges absolutely in the sense that
As a complete normed space, Hilbert spaces are by definition also Banach spaces. As such they are topological vector spaces, in which topological notions like the openness and closedness of subsets are well-defined. Of special importance is the notion of a closed linear subspace of a Hilbert space which, with the inner product induced by restriction, is also complete (being a closed set in a complete metric space) and therefore a Hilbert space in its own right.
Completeness of the space holds provided that whenever a series of elements from ℓ2 converges absolutely (in norm), then it converges to an element of ℓ2. The proof is basic in mathematical analysis, and permits mathematical series of elements of the space to be manipulated with the same ease as series of complex numbers (or vectors in a finite-dimensional Euclidean space).[5]
In the first decade of the 20th century, parallel developments led to the introduction of Hilbert spaces. The first of these was the observation, which arose during David Hilbert and Erhard Schmidt's study of integral equations,[8] that two square-integrable real-valued functions f and g on an interval [a,b] have an inner product
The second development was the Lebesgue integral, an alternative to the Riemann integral introduced by Henri Lebesgue in 1904.[10] The Lebesgue integral made it possible to integrate a much broader class of functions. In 1907, Frigyes Riesz and Ernst Sigismund Fischer independently proved that the space L2 of square Lebesgue-integrable functions is a complete metric space.[11] As a consequence of the interplay between geometry and completeness, the 19th century results of Joseph Fourier, Friedrich Bessel and Marc-Antoine Parseval on trigonometric series easily carried over to these more general spaces, resulting in a geometrical and analytical apparatus now usually known as the Riesz-Fischer theorem.[12]
Further basic results were proved in the early 20th century. For example, the Riesz representation theorem was independently established by Maurice Fréchet and Frigyes Riesz in 1907.[13] John von Neumann coined the term abstract Hilbert space in his work on unbounded Hermitian operators.[14] Although other mathematicians such as Hermann Weyl and Norbert Wiener had already studied particular Hilbert spaces in great detail, often from a physically-motivated point of view, von Neumann gave the first complete and axiomatic treatment of them.[15] Von Neumann later used them in his seminal work on the foundations of quantum mechanics,[16] and in his continued work with Eugene Wigner. The name "Hilbert space" was soon adopted by others, for example by Hermann Weyl in his book on quantum mechanics and the theory of groups.[17]
The significance of the concept of a Hilbert space was underlined with the realization that it offers one of the best mathematical formulations of quantum mechanics.[18] In short, the states of a quantum mechanical system are vectors in a certain Hilbert space, the observables are hermitian operators on that space, the symmetries of the system are unitary operators, and measurements are orthogonal projections. The relation between quantum mechanical symmetries and unitary operators provided an impetus for the development of the unitary representation theory of groups, initiated in the 1928 work of Hermann Weyl.[17] On the other hand, in the early 1930s it became clear that certain properties of classical dynamical systems can be analyzed using Hilbert space techniques in the framework of ergodic theory.[19]
The algebra of observables in quantum mechanics is naturally an algebra of operators defined on a Hilbert space, according to Werner Heisenberg's matrix mechanics formulation of quantum theory. Von Neumann began investigating operator algebras in the 1930s, as rings of operators on a Hilbert space. The kind of algebras studied by von Neumann and his contemporaries are now known as von Neumann algebras. In the 1940s, Israel Gelfand, Mark Naimark and Irving Segal gave a definition of a kind of operator algebras called C*-algebras that on the one hand made no reference to an underlying Hilbert space, and on the other extrapolated many of the useful features of the operator algebras that had previously been studied. The spectral theorem for self-adjoint operators in particular that underlies much of the existing Hilbert space theory was generalized to C*-algebras. These techniques are now basic in abstract harmonic analysis and representation theory.
The inner product of functions f and g in L2(X,μ) is then defined as
The Lebesgue spaces appear in many natural settings. The spaces L2(R) and L2([0,1]) of square-integrable functions with respect to the Lebesgue measure on the real line and unit interval, respectively, are natural domains on which to define the Fourier transform and Fourier series. In other situations, the measure may be something other than the ordinary Lebesgue measure on the real line. For instance, if w is any positive measurable function, the space of all measurable functions f on the interval [0,1] satisfying
w([0,1]), and w is called the weight function. The inner product is defined by
w([0,1]) is identical with the Hilbert space L2([0,1],μ) where the measure μ of a Lebesgue-measurable set A is defined by
For s a non-negative integer and Ω ⊂ Rn, the Sobolev space Hs(Ω) contains L2 functions whose weak derivatives of order up to s are also L2. The inner product in Hs(Ω) is
Sobolev spaces are also studied from the point of view of spectral theory, relying more specifically on the Hilbert space structure. If Ω is a suitable domain, then one can define the Sobolev space Hs(Ω) as the space of Bessel potentials;[24] roughly,

In the theory of ordinary differential equations, spectral methods on a suitable Hilbert space are used to study the behavior of eigenvalues and eigenfunctions of differential equations. For example, the Sturm–Liouville problem arises in the study of the harmonics of waves in a violin string or a drum, and is a central problem in ordinary differential equations.[29] The problem is a differential equation of the form
A typical example is the Poisson equation −Δu = g with Dirichlet boundary conditions in a bounded domain Ω in R2. The weak formulation consists of finding a function u such that, for all continuously differentiable functions v in Ω vanishing on the boundary:
0(Ω) consisting of functions u such that u, along with its weak partial derivatives, are square integrable on Ω, and which vanish on the boundary. The question then reduces to finding u in this space such that for all v in this space
Hilbert spaces allow for many elliptic partial differential equations to be formulated in a similar way, and the Lax-Milgram theorem is then a basic tool in their analysis. With suitable modifications, similar techniques can be applied to parabolic partial differential equations and certain hyperbolic partial differential equations.
An ergodic dynamical system is one for which, apart from the energy—measured by the Hamiltonian—there are no other functionally independent conserved quantities on the phase space. More explicitly, suppose that the energy E is fixed, and let ΩE be the subset of the phase space consisting of all states of energy E (an energy surface), and let Tt denote the evolution operator on the phase space. The dynamical system is ergodic if there are no continuous non-constant functions on ΩE such that

One of the basic goals of Fourier analysis is to decompose a function into a (possibly infinite) linear combination of given basis functions: the associated Fourier series. The classical Fourier series associated to a function ƒ defined on the interval [0,1] is a series of the form
A significant problem in classical Fourier series asks in what sense the Fourier series converges, if at all, to the function ƒ. Hilbert space methods provide one possible answer to this question.[33] The functions en(θ) = e2πinθ form an orthogonal basis of the Hilbert space L2([0,1]). Consequently, any square-integrable function can be expressed as a series
The problem can also be studied from the abstract point of view: every Hilbert space has an orthonormal basis, and every element of the Hilbert space can be written in a unique way as a sum of multiples of these basis elements. The coefficients appearing on these basis elements are sometimes known abstractly as the Fourier coefficients of the element of the space.[34] The abstraction is especially useful when it is more natural to use different basis functions for a space such as L2([0,1]). In many circumstances, it is desirable not to decompose a function into trigonometric functions, but rather into orthogonal polynomials or wavelets for instance,[35] and in higher dimensions into spherical harmonics.[36]
For instance, if en are any orthonormal basis functions of L2[0,1], then a given function in L2[0,1] can be approximated as a finite linear combination[37]
In various applications to physical problems, a function can be decomposed into physically meaningful eigenfunctions of a differential operator (typically the Laplace operator): this forms the foundation for the spectral study of functions, in reference to the spectrum of the differential operator.[39] A concrete physical application involves the problem of hearing the shape of a drum: given the fundamental modes of vibration that a drumhead is capable of producing, can one infer the shape of the drum itself?[40] The mathematical formulation of this question involves the Dirichlet eigenvalues of the Laplace equation in the plane, that represent the fundamental modes of vibration in direct analogy with the integers that represent the fundamental modes of vibration of the violin string.
Spectral theory also underlies certain aspects of the Fourier transform of a function. Whereas Fourier analysis decomposes a function defined on a compact set into the discrete spectrum of the Laplacian (which corresponds to the vibrations of a violin string or drum), the Fourier transform of a function is the decomposition of a function defined on all of Euclidean space into its components in the continuous spectrum of the Laplacian. The Fourier transformation is also geometrical, in a sense made precise by the Plancherel theorem, that asserts that it is an isometry of one Hilbert space (the "time domain") with another (the "frequency domain"). This isometry property of the Fourier transformation is a recurring theme in abstract harmonic analysis, as evidenced for instance by the Plancherel theorem for spherical functions occurring in noncommutative harmonic analysis.
The time evolution of a quantum state is described by the Schrödinger equation, in which the Hamiltonian, the operator corresponding to the total energy of the system, generates time evolution.
The inner product between two state vectors is a complex number known as a probability amplitude. During an ideal measurement of a quantum mechanical system, the probability that a system collapses from a given initial state to a particular eigenstate is given by the square of the absolute value of the probability amplitudes between the initial and final states. The possible results of a measurement are the eigenvalues of the operator—which explains the choice of self-adjoint operators, for all the eigenvalues must be real. The probability distribution of an observable in a given state can be found by computing the spectral decomposition of the corresponding operator.
For a general system, states are typically not pure, but instead are represented as statistical mixtures of pure states, or mixed states, given by density matrices: self-adjoint operators of trace one on a Hilbert space. Moreover, for general quantum mechanical systems, the effects of a single measurement can influence other parts of a system in a manner that is described instead by a positive operator valued measure. Thus the structure both of the states and observables in the general theory is considerably more complicated than the idealization for pure states.
Heisenberg's uncertainty principle is represented by the statement that the operators corresponding to certain observables do not commute, and gives a specific form that the commutator must have.
 = 0. The notation for this is u ⊥ v. More generally, when S is a subset in H, the notation u ⊥ S means that u is orthogonal to every element from S.
= 0. The notation for this is u ⊥ v. More generally, when S is a subset in H, the notation u ⊥ S means that u is orthogonal to every element from S.
When u and v are orthogonal, one has
When this result is applied to a closed subspace F of H, it can be shown that the point y ∈ F closest to x is characterized by[47]
In particular, when F is not equal to H, one can find a non-zero vector v orthogonal to F (select x not in F and v = x − y). A very useful criterion is obtained by applying this observation to the closed subspace F generated by a subset S of H.
The Riesz representation theorem affords a convenient description of the dual. To every element u of H, there is a unique element φu of H∗, defined by
 is an antilinear mapping from H to H∗. The Riesz representation theorem states that this mapping is an antilinear isomorphism.[48] Thus to every element φ of the dual H∗ there exists one and only one uφ in H such that
is an antilinear mapping from H to H∗. The Riesz representation theorem states that this mapping is an antilinear isomorphism.[48] Thus to every element φ of the dual H∗ there exists one and only one uφ in H such that
The representing vector uφ is obtained in the following way. When φ ≠ 0, the kernel F = ker φ is a closed vector subspace of H, not equal to H, hence there exists a non-zero vector v orthogonal to F. The vector u is a suitable scalar multiple λv of v. The requirement that φ(v) = 〈v, u〉 yields
The Riesz representation theorem relies fundamentally not just on the presence of an inner product, but also on the completeness of the space. In fact, the theorem implies that the topological dual of any inner product space can be identified with its completion. An immediate consequence of the Riesz representation theorem is also that a Hilbert space H is reflexive, meaning that the natural map from H into its double dual space is an isomorphism.
For example, any orthonormal sequence {ƒn} converges weakly to 0, as a consequence of Bessel's inequality. Every weakly convergent sequence {xn} is bounded, by the uniform boundedness principle.
Conversely, every bounded sequence in a Hilbert space admits weakly convergent subsequences (Alaoglu's theorem).[49] This fact may be used to prove minimization results for continuous convex functionals, in the same way that the Bolzano-Weierstrass theorem is used for continuous functions on Rd. Among several variants, one simple statement is as follows:[50]
The (geometrical) Hahn–Banach theorem asserts that a closed convex set can be separated from any point outside it by means of a hyperplane of the Hilbert space. This is an immediate consequence of the best approximation property: if y is the element of a closed convex set F closest to x, then the separating hyperplane is the plane perpendicular to the segment xy passing through its midpoint.[53]
The set B(H) of all bounded linear operators on H, together with the addition and composition operations, the norm and the adjoint operation, is a C*-algebra, which is a type of operator algebra.
An element A of B(H) is called self-adjoint or Hermitian if A∗ = A. If A is Hermitian and 〈Ax, x〉 ≥ 0 for every x, then A is called non-negative, written A ≥ 0; if equality holds only when x = 0, then A is called positive. The set of self adjoint operators admits a partial order, in which A ≥ B if A − B ≥ 0. If A has the form B∗B for some B, then A is non-negative; if B is invertible, then A is positive. A converse is also true in the sense that, for a non-negative operator A, there exists a unique non-negative square root B such that
An element U of B(H) is called unitary if U is invertible and its inverse is given by U∗. This can also be expressed by requiring that U be onto and〈Ux, Uy〉 =〈x, y〉 for all x and y in H. The unitary operators form a group under composition, which is the isometry group of H.
An element of B(H) is compact if it sends bounded sets to relatively compact sets. Equivalently, a bounded operator T is compact if, for any bounded sequence {xk}, the sequence {Txk} has a convergent subsequence. Many integral operators are compact, and in fact define a special class of operators known as Hilbert–Schmidt operators that are especially important in the study of integral equations. Fredholm operators are those which differ from a compact operator by a multiple of the identity, and are equivalently characterized as operators with a finite dimensional kernel and cokernel. The index of a Fredholm operator T is defined by
The adjoint of a densely defined unbounded operator is defined in essentially the same manner as for bounded operators. Self-adjoint unbounded operators play the role of the observables in the mathematical formulation of quantum mechanics. Examples of self-adjoint unbounded operators on the Hilbert space L2(R) are:[55]
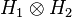 . The Hilbertian tensor product of H1 and H2, sometimes denoted by
. The Hilbertian tensor product of H1 and H2, sometimes denoted by 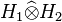 , is the Hilbert space obtained by completing
, is the Hilbert space obtained by completing 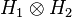 for the metric associated to this inner product.[57]
for the metric associated to this inner product.[57]
An example is provided by the Hilbert space L2([0, 1]). The Hilbertian tensor product of two copies of L2([0, 1]) is isometrically and linearly isomorphic to the space L2([0, 1]2) of square-integrable functions on the square [0, 1]2. This isomorphism sends a simple tensor to the function
to the function
This example is typical in the following sense.[58] Associated to every simple tensor product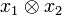 is the rank one operator
is the rank one operator
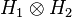 and the space of finite rank operators from H1∗ to H2. This extends to a linear isometry of the Hilbertian tensor product
and the space of finite rank operators from H1∗ to H2. This extends to a linear isometry of the Hilbertian tensor product 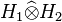 with the Hilbert space HS(H1∗, H2) of Hilbert-Schmidt operators from H1∗ to H2.
with the Hilbert space HS(H1∗, H2) of Hilbert-Schmidt operators from H1∗ to H2.
Examples of orthonormal bases include:
An orthonormal basis of ℓ 2(B) is indexed by the set B, given by
Geometrically, Bessel's inequality implies that the orthogonal projection of x onto the linear subspace spanned by the fi has norm that does not exceed that of x. In two dimensions, this is the assertion that the length of the leg of a right triangle may not exceed the length of the hypotenuse.
Bessel's inequality is a stepping stone to the more powerful Parseval identity which governs the case when Bessel's inequality is actually an equality. If {ek}k ∈ B is an orthonormal basis of H, then every element x of H may be written as
As a consequence of Parseval's identity, if {ek}k ∈ B is an orthonormal basis of H, then the map Φ : H → ℓ2(B) defined by Φ(x) = (〈x,ek〉)k∈B is an isometric isomorphism of Hilbert spaces: it is a bijective linear mapping such that
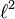 .
.
In the past, Hilbert spaces were often required to be separable as part of the definition.[62] Most spaces used in physics are separable, and since these are all isomorphic to each other, one often refers to any infinite-dimensional separable Hilbert space as "the Hilbert space" or just "Hilbert space".[63] Even in quantum field theory, most of the Hilbert spaces are in fact separable, as stipulated by the Wightman axioms. However, it is sometimes argued that non-separable Hilbert spaces are also important in quantum field theory, roughly because the systems in the theory possess an infinite number of degrees of freedom and any infinite Hilbert tensor product (of spaces of dimension greater than one) is non-separable.[64] For instance, a bosonic field can be naturally thought of as an element of a tensor product whose factors represent harmonic oscillators at each point of space. From this perspective, the natural state space of a boson might seem to be a non-separable space.[64] However, it is only a small separable subspace of the full tensor product that can contain physically meaningful fields (on which the observables can be defined). Another non-separable Hilbert space models the state of an infinite collection of particles in an unbounded region of space. An orthonormal basis of the space is indexed by the density of the particles, a continuous parameter, and since the set of possible densities is uncountable, the basis is not countable.[64]
The linear operator PV : H → H which maps x to v is called the orthogonal projection onto V. There is a natural one-to-one correspondence between the set of all closed subspaces of H and the set of all bounded self-adjoint operators P such that P2 = P. Specifically,
An operator P such that P = P2 = P∗ is called an orthogonal projection. The orthogonal projection PV onto a closed subspace V of H is the adjoint of the inclusion mapping
The operator norm of a projection P onto a non-zero closed subspace is equal to one:
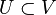 , then
, then  with equality holding if and only if V is contained in the closure of U. This result is a special case of the Hahn–Banach theorem. The closure of a subspace can be completely characterized in terms of the orthogonal complement: If V is a subspace of H, then the closure of V is equal to
with equality holding if and only if V is contained in the closure of U. This result is a special case of the Hahn–Banach theorem. The closure of a subspace can be completely characterized in terms of the orthogonal complement: If V is a subspace of H, then the closure of V is equal to  . The orthogonal complement is thus a Galois connection on the partial order of subspaces of a Hilbert space. In general, the orthogonal complement of a sum of subspaces is the intersection of the orthogonal complements:[68]
. The orthogonal complement is thus a Galois connection on the partial order of subspaces of a Hilbert space. In general, the orthogonal complement of a sum of subspaces is the intersection of the orthogonal complements:[68]  . If the Vi are in addition closed, then
. If the Vi are in addition closed, then  .
.
The spectrum of an operator T, denoted σ(T) is the set of complex numbers λ such that T − λ lacks a continuous inverse. If T is bounded, then the spectrum is always a compact set in the complex plane, and lies inside the disc If T is self-adjoint, then the spectrum is real. In fact, it is contained in the interval [m,M] where
If T is self-adjoint, then the spectrum is real. In fact, it is contained in the interval [m,M] where
The eigenspaces of an operator T are given by
However, the spectral theorem of a self-adjoint operator T takes a particularly simple form if, in addition, T is assumed to be a compact operator. The spectral theorem for compact self-adjoint operators states:[70]
The general spectral theorem for self-adjoint operators involves a kind of operator-valued Riemann–Stieltjes integral, rather than an infinite summation.[71] The spectral family associated to T associates to each real number λ an operator Eλ, which is the projection onto the nullspace of the operator (T − λ) + , where the positive part of a self-adjoint operator is defined by
A major application of spectral methods is the spectral mapping theorem, which allows one to apply to a self-adjoint operator T any continuous complex function ƒ defined on the spectrum of T by forming the integral
The spectral theory of unbounded self-adjoint operators is only marginally more difficult than for bounded operators. The spectrum of an unbounded operator is defined in precisely the same way as for bounded operators: λ is a spectral value if the resolvent operator
A precise version of the spectral theorem which holds in this case is:[73]
literally copied from : http://en.wikipedia.org/wiki/Hilbert_space
Hilbert spaces arise naturally and frequently in mathematics, physics, and engineering, typically as infinite-dimensional function spaces. The earliest Hilbert spaces were studied from this point of view in the first decade of the 20th century by David Hilbert, Erhard Schmidt, and Frigyes Riesz. They are indispensable tools in the theories of partial differential equations, quantum mechanics, Fourier analysis (which includes applications to signal processing and heat transfer) and ergodic theory which forms the mathematical underpinning of the study of thermodynamics. John von Neumann coined the term "Hilbert space" for the abstract concept underlying many of these diverse applications. The success of Hilbert space methods ushered in a very fruitful era for functional analysis. Apart from the classical Euclidean spaces, examples of Hilbert spaces include spaces of square-integrable functions, spaces of sequences, Sobolev spaces consisting of generalized functions, and Hardy spaces of holomorphic functions.
Geometric intuition plays an important role in many aspects of Hilbert space theory. Exact analogs of the Pythagorean theorem and parallelogram law hold in a Hilbert space. At a deeper level, perpendicular projection onto a subspace (the analog of "dropping the altitude" of a triangle) plays a significant role in optimization problems and other aspects of the theory. An element of a Hilbert space can be uniquely specified by its coordinates with respect to a set of coordinate axes (an orthonormal basis), in analogy with Cartesian coordinates in the plane. When that set of axes is countably infinite, this means that the Hilbert space can also usefully be thought of in terms of infinite sequences that are square-summable. Linear operators on a Hilbert space are likewise fairly concrete objects: in good cases, they are simply transformations that stretch the space by different factors in mutually perpendicular directions in a sense that is made precise by the study of their spectrum.
Contents[hide] |
[edit] Definition and illustration
[edit] Motivating example: Euclidean space
One of the most familiar examples of a Hilbert space is the Euclidean space consisting of three-dimensional vectors, denoted by R3, and equipped with the dot product. The dot product takes two vectors x and y, and produces a real number x·y. If x and y are represented in Cartesian coordinates, then the dot product is defined by- It is symmetric in x and y: x·y = y·x.
- It is linear in its first argument: (ax1 + bx2)·y = ax1·y + bx2·y for any scalars a, b, and vectors x1, x2, and y.
- It is positive definite: for all vectors x, x·x ≥ 0 with equality if and only if x = 0.
Multivariable calculus in Euclidean space relies on the ability to compute limits, and to have useful criteria for concluding that limits exist. A mathematical series
[edit] Definition
A Hilbert space H is a real or complex inner product space that is also a complete metric space with respect to the distance function induced by the inner product.[2] To say that H is a complex inner product space means that H is a complex vector space on which there is an inner product 〈x,y〉 associating a complex number to each pair of elements x,y of H that satisfies the following properties:- 〈y,x〉 is the complex conjugate of 〈x,y〉:
- The inner product 〈•,•〉 is positive definite:
-
- where the case of equality holds precisely when x = 0.
The norm defined by the inner product 〈•,•〉 is the real-valued function
Relative to a distance function defined in this way, any inner product space is a metric space, and sometimes is known as a pre-Hilbert space.[4] A pre-Hilbert space is a Hilbert space if in addition it is complete. Completeness is expressed using a form of the Cauchy criterion for sequences in H: a pre-Hilbert space H is complete if every Cauchy sequence converges with respect to this norm to an element in the space. Completeness can be characterized by the following equivalent condition: if a series of vectors
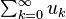 converges absolutely in the sense that
converges absolutely in the sense thatAs a complete normed space, Hilbert spaces are by definition also Banach spaces. As such they are topological vector spaces, in which topological notions like the openness and closedness of subsets are well-defined. Of special importance is the notion of a closed linear subspace of a Hilbert space which, with the inner product induced by restriction, is also complete (being a closed set in a complete metric space) and therefore a Hilbert space in its own right.
[edit] Second example: sequence spaces
The sequence space ℓ2 consists of all infinite sequences z = (z1,z2,...) of complex numbers such that the seriesCompleteness of the space holds provided that whenever a series of elements from ℓ2 converges absolutely (in norm), then it converges to an element of ℓ2. The proof is basic in mathematical analysis, and permits mathematical series of elements of the space to be manipulated with the same ease as series of complex numbers (or vectors in a finite-dimensional Euclidean space).[5]
[edit] History
Prior to the development of Hilbert spaces, other generalizations of Euclidean spaces were known to mathematicians and physicists. In particular, the idea of an abstract linear space had gained some traction towards the end of the 19th century:[6] this is a space whose elements can be added together and multiplied by scalars (such as real or complex numbers) without necessarily identifying these elements with "geometric" vectors, such as position and momentum vectors in physical systems. Other objects studied by mathematicians at the turn of the 20th century, in particular spaces of sequences (including series) and spaces of functions,[7] can naturally be thought of as linear spaces. Functions, for instance, can be added together or multiplied by constant scalars, and these operations obey the algebraic laws satisfied by addition and scalar multiplication of spatial vectors.In the first decade of the 20th century, parallel developments led to the introduction of Hilbert spaces. The first of these was the observation, which arose during David Hilbert and Erhard Schmidt's study of integral equations,[8] that two square-integrable real-valued functions f and g on an interval [a,b] have an inner product
The second development was the Lebesgue integral, an alternative to the Riemann integral introduced by Henri Lebesgue in 1904.[10] The Lebesgue integral made it possible to integrate a much broader class of functions. In 1907, Frigyes Riesz and Ernst Sigismund Fischer independently proved that the space L2 of square Lebesgue-integrable functions is a complete metric space.[11] As a consequence of the interplay between geometry and completeness, the 19th century results of Joseph Fourier, Friedrich Bessel and Marc-Antoine Parseval on trigonometric series easily carried over to these more general spaces, resulting in a geometrical and analytical apparatus now usually known as the Riesz-Fischer theorem.[12]
Further basic results were proved in the early 20th century. For example, the Riesz representation theorem was independently established by Maurice Fréchet and Frigyes Riesz in 1907.[13] John von Neumann coined the term abstract Hilbert space in his work on unbounded Hermitian operators.[14] Although other mathematicians such as Hermann Weyl and Norbert Wiener had already studied particular Hilbert spaces in great detail, often from a physically-motivated point of view, von Neumann gave the first complete and axiomatic treatment of them.[15] Von Neumann later used them in his seminal work on the foundations of quantum mechanics,[16] and in his continued work with Eugene Wigner. The name "Hilbert space" was soon adopted by others, for example by Hermann Weyl in his book on quantum mechanics and the theory of groups.[17]
The significance of the concept of a Hilbert space was underlined with the realization that it offers one of the best mathematical formulations of quantum mechanics.[18] In short, the states of a quantum mechanical system are vectors in a certain Hilbert space, the observables are hermitian operators on that space, the symmetries of the system are unitary operators, and measurements are orthogonal projections. The relation between quantum mechanical symmetries and unitary operators provided an impetus for the development of the unitary representation theory of groups, initiated in the 1928 work of Hermann Weyl.[17] On the other hand, in the early 1930s it became clear that certain properties of classical dynamical systems can be analyzed using Hilbert space techniques in the framework of ergodic theory.[19]
The algebra of observables in quantum mechanics is naturally an algebra of operators defined on a Hilbert space, according to Werner Heisenberg's matrix mechanics formulation of quantum theory. Von Neumann began investigating operator algebras in the 1930s, as rings of operators on a Hilbert space. The kind of algebras studied by von Neumann and his contemporaries are now known as von Neumann algebras. In the 1940s, Israel Gelfand, Mark Naimark and Irving Segal gave a definition of a kind of operator algebras called C*-algebras that on the one hand made no reference to an underlying Hilbert space, and on the other extrapolated many of the useful features of the operator algebras that had previously been studied. The spectral theorem for self-adjoint operators in particular that underlies much of the existing Hilbert space theory was generalized to C*-algebras. These techniques are now basic in abstract harmonic analysis and representation theory.
[edit] Examples
[edit] Lebesgue spaces
Main article: Lp space
Lebesgue spaces are function spaces associated to measure spaces (X, M, μ), where X is a set, M is a σ-algebra of subsets of X, and μ is a countably additive measure on M. Let L2(X,μ) be the space of those complex-valued measurable functions on X for which the Lebesgue integral of the square of the absolute value of the function is finite, i.e., for a function f in L2(X,μ),The inner product of functions f and g in L2(X,μ) is then defined as
The Lebesgue spaces appear in many natural settings. The spaces L2(R) and L2([0,1]) of square-integrable functions with respect to the Lebesgue measure on the real line and unit interval, respectively, are natural domains on which to define the Fourier transform and Fourier series. In other situations, the measure may be something other than the ordinary Lebesgue measure on the real line. For instance, if w is any positive measurable function, the space of all measurable functions f on the interval [0,1] satisfying
w([0,1]), and w is called the weight function. The inner product is defined by
w([0,1]) is identical with the Hilbert space L2([0,1],μ) where the measure μ of a Lebesgue-measurable set A is defined by
[edit] Sobolev spaces
Sobolev spaces, denoted by Hs or W s, 2, are Hilbert spaces. These are a special kind of function space in which differentiation may be performed, but which (unlike other Banach spaces such as the Hölder spaces) support the structure of an inner product. Because differentiation is permitted, Sobolev spaces are a convenient setting for the theory of partial differential equations.[22] They also form the basis of the theory of direct methods in the calculus of variations.[23]For s a non-negative integer and Ω ⊂ Rn, the Sobolev space Hs(Ω) contains L2 functions whose weak derivatives of order up to s are also L2. The inner product in Hs(Ω) is
Sobolev spaces are also studied from the point of view of spectral theory, relying more specifically on the Hilbert space structure. If Ω is a suitable domain, then one can define the Sobolev space Hs(Ω) as the space of Bessel potentials;[24] roughly,
[edit] Spaces of holomorphic functions
- Hardy spaces
- Bergman spaces
[edit] Applications
Many of the applications of Hilbert spaces exploit the fact that Hilbert spaces support generalizations of simple geometric concepts like projection and change of basis from their usual finite dimensional setting. In particular, the spectral theory of continuous self-adjoint linear operators on a Hilbert space generalizes the usual spectral decomposition of a matrix, and this often plays a major role in applications of the theory to other areas of mathematics and physics.[edit] Sturm–Liouville theory
Main articles: Sturm–Liouville theory and Spectral theory of ordinary differential equations

The overtones of a vibrating string. These are eigenfunctions of an associated Sturm–Liouville problem. The eigenvalues 1,1/2,1/3,… form the (musical) harmonic series.
[edit] Partial differential equations
Hilbert spaces form a basic tool in the study of partial differential equations.[22] For many classes of partial differential equations, such as linear elliptic equations, it is possible to consider a generalized solution (known as a weak solution) by enlarging the class of functions. Many weak formulations involve the class of Sobolev functions, which is a Hilbert space. A suitable weak formulation reduces to a geometrical problem the analytic problem of finding a solution or, often what is more important, showing that a solution exists and is unique for given boundary data. For linear elliptic equations, one geometrical result that ensures unique solvability for a large class of problems is the Lax–Milgram theorem. This strategy forms the rudiment of the Galerkin method (a finite element method) for numerical solution of partial differential equations.[31]A typical example is the Poisson equation −Δu = g with Dirichlet boundary conditions in a bounded domain Ω in R2. The weak formulation consists of finding a function u such that, for all continuously differentiable functions v in Ω vanishing on the boundary:
0(Ω) consisting of functions u such that u, along with its weak partial derivatives, are square integrable on Ω, and which vanish on the boundary. The question then reduces to finding u in this space such that for all v in this space
- a(u,v) = b(v)
Hilbert spaces allow for many elliptic partial differential equations to be formulated in a similar way, and the Lax-Milgram theorem is then a basic tool in their analysis. With suitable modifications, similar techniques can be applied to parabolic partial differential equations and certain hyperbolic partial differential equations.
[edit] Ergodic theory
The field of ergodic theory is the study of the long-term behavior of chaotic dynamical systems. The protypical case of a field to which ergodic theory is applicable is that of thermodynamics in which, although the microscopic state of a system is extremely complicated—it is impossible to understand the ensemble of individual collisions between particles of matter—the average behavior over sufficiently long time intervals is tractable. The laws of thermodynamics are assertions about such average behavior. In particular, one formulation of the zeroth law of thermodynamics asserts that over sufficiently long timescales, the only functionally independent measurement that one can make of a thermodynamic system in equilibrium is its total energy, in the form of temperature.
An ergodic dynamical system is one for which, apart from the energy—measured by the Hamiltonian—there are no other functionally independent conserved quantities on the phase space. More explicitly, suppose that the energy E is fixed, and let ΩE be the subset of the phase space consisting of all states of energy E (an energy surface), and let Tt denote the evolution operator on the phase space. The dynamical system is ergodic if there are no continuous non-constant functions on ΩE such that
- If Ut is a (strongly continuous) one-parameter semigroup of unitary operators on a Hilbert space H, and P is the orthogonal projection onto the space of common fixed points of Ut, {x∈H | Utx = x for all t > 0}, then
[edit] Fourier analysis

Spherical harmonics, an orthonormal basis for the Hilbert space of square-integrable functions on the sphere, shown graphed along the radial direction
A significant problem in classical Fourier series asks in what sense the Fourier series converges, if at all, to the function ƒ. Hilbert space methods provide one possible answer to this question.[33] The functions en(θ) = e2πinθ form an orthogonal basis of the Hilbert space L2([0,1]). Consequently, any square-integrable function can be expressed as a series
The problem can also be studied from the abstract point of view: every Hilbert space has an orthonormal basis, and every element of the Hilbert space can be written in a unique way as a sum of multiples of these basis elements. The coefficients appearing on these basis elements are sometimes known abstractly as the Fourier coefficients of the element of the space.[34] The abstraction is especially useful when it is more natural to use different basis functions for a space such as L2([0,1]). In many circumstances, it is desirable not to decompose a function into trigonometric functions, but rather into orthogonal polynomials or wavelets for instance,[35] and in higher dimensions into spherical harmonics.[36]
For instance, if en are any orthonormal basis functions of L2[0,1], then a given function in L2[0,1] can be approximated as a finite linear combination[37]
In various applications to physical problems, a function can be decomposed into physically meaningful eigenfunctions of a differential operator (typically the Laplace operator): this forms the foundation for the spectral study of functions, in reference to the spectrum of the differential operator.[39] A concrete physical application involves the problem of hearing the shape of a drum: given the fundamental modes of vibration that a drumhead is capable of producing, can one infer the shape of the drum itself?[40] The mathematical formulation of this question involves the Dirichlet eigenvalues of the Laplace equation in the plane, that represent the fundamental modes of vibration in direct analogy with the integers that represent the fundamental modes of vibration of the violin string.
Spectral theory also underlies certain aspects of the Fourier transform of a function. Whereas Fourier analysis decomposes a function defined on a compact set into the discrete spectrum of the Laplacian (which corresponds to the vibrations of a violin string or drum), the Fourier transform of a function is the decomposition of a function defined on all of Euclidean space into its components in the continuous spectrum of the Laplacian. The Fourier transformation is also geometrical, in a sense made precise by the Plancherel theorem, that asserts that it is an isometry of one Hilbert space (the "time domain") with another (the "frequency domain"). This isometry property of the Fourier transformation is a recurring theme in abstract harmonic analysis, as evidenced for instance by the Plancherel theorem for spherical functions occurring in noncommutative harmonic analysis.
[edit] Quantum mechanics
In the mathematically rigorous formulation of quantum mechanics, developed by Paul Dirac[41] and John von Neumann[42], the possible states (more precisely, the pure states) of a quantum mechanical system are represented by unit vectors (called state vectors) residing in a complex separable Hilbert space, known as the state space, well defined up to a complex number of norm 1 (the phase factor). In other words, the possible states are points in the projectivization of a Hilbert space, usually called the complex projective space. The exact nature of this Hilbert space is dependent on the system; for example, the position and momentum states for a single non-relativistic spin zero particle is the space of all square-integrable functions, while the states for the spin of a single proton are unit elements of the two-dimensional complex Hilbert space of spinors. Each observable is represented by a self-adjoint linear operator acting on the state space. Each eigenstate of an observable corresponds to an eigenvector of the operator, and the associated eigenvalue corresponds to the value of the observable in that eigenstate.
The time evolution of a quantum state is described by the Schrödinger equation, in which the Hamiltonian, the operator corresponding to the total energy of the system, generates time evolution.
The inner product between two state vectors is a complex number known as a probability amplitude. During an ideal measurement of a quantum mechanical system, the probability that a system collapses from a given initial state to a particular eigenstate is given by the square of the absolute value of the probability amplitudes between the initial and final states. The possible results of a measurement are the eigenvalues of the operator—which explains the choice of self-adjoint operators, for all the eigenvalues must be real. The probability distribution of an observable in a given state can be found by computing the spectral decomposition of the corresponding operator.
For a general system, states are typically not pure, but instead are represented as statistical mixtures of pure states, or mixed states, given by density matrices: self-adjoint operators of trace one on a Hilbert space. Moreover, for general quantum mechanical systems, the effects of a single measurement can influence other parts of a system in a manner that is described instead by a positive operator valued measure. Thus the structure both of the states and observables in the general theory is considerably more complicated than the idealization for pure states.
Heisenberg's uncertainty principle is represented by the statement that the operators corresponding to certain observables do not commute, and gives a specific form that the commutator must have.
[edit] Properties
[edit] Pythagorean identity
Two vectors u and v in a Hilbert space H are orthogonal when = 0. The notation for this is u ⊥ v. More generally, when S is a subset in H, the notation u ⊥ S means that u is orthogonal to every element from S.
= 0. The notation for this is u ⊥ v. More generally, when S is a subset in H, the notation u ⊥ S means that u is orthogonal to every element from S.When u and v are orthogonal, one has
[edit] Parallelogram identity and polarization
By definition, every Hilbert space is also a Banach space. Furthermore, in every Hilbert space the following parallelogram identity holds:
[edit] Best approximation
If C is a non-empty closed convex subset of a Hilbert space H and x a point in H, there exists a unique point y ∈ C which minimizes the distance between x and points in C,[45]When this result is applied to a closed subspace F of H, it can be shown that the point y ∈ F closest to x is characterized by[47]
In particular, when F is not equal to H, one can find a non-zero vector v orthogonal to F (select x not in F and v = x − y). A very useful criterion is obtained by applying this observation to the closed subspace F generated by a subset S of H.
- A subset S of H spans a dense vector subspace if (and only if) the vector 0 is the sole vector v ∈ H orthogonal to S.
[edit] Duality
The dual space H∗ is the space of all continuous linear functions from the space H into the base field. It carries a natural norm, defined byThe Riesz representation theorem affords a convenient description of the dual. To every element u of H, there is a unique element φu of H∗, defined by
 is an antilinear mapping from H to H∗. The Riesz representation theorem states that this mapping is an antilinear isomorphism.[48] Thus to every element φ of the dual H∗ there exists one and only one uφ in H such that
is an antilinear mapping from H to H∗. The Riesz representation theorem states that this mapping is an antilinear isomorphism.[48] Thus to every element φ of the dual H∗ there exists one and only one uφ in H such thatThe representing vector uφ is obtained in the following way. When φ ≠ 0, the kernel F = ker φ is a closed vector subspace of H, not equal to H, hence there exists a non-zero vector v orthogonal to F. The vector u is a suitable scalar multiple λv of v. The requirement that φ(v) = 〈v, u〉 yields
The Riesz representation theorem relies fundamentally not just on the presence of an inner product, but also on the completeness of the space. In fact, the theorem implies that the topological dual of any inner product space can be identified with its completion. An immediate consequence of the Riesz representation theorem is also that a Hilbert space H is reflexive, meaning that the natural map from H into its double dual space is an isomorphism.
[edit] Weakly convergent sequences
Main article: Weak convergence (Hilbert space)
In a Hilbert space H, a sequence {xn} is weakly convergent to a vector x ∈ H whenFor example, any orthonormal sequence {ƒn} converges weakly to 0, as a consequence of Bessel's inequality. Every weakly convergent sequence {xn} is bounded, by the uniform boundedness principle.
Conversely, every bounded sequence in a Hilbert space admits weakly convergent subsequences (Alaoglu's theorem).[49] This fact may be used to prove minimization results for continuous convex functionals, in the same way that the Bolzano-Weierstrass theorem is used for continuous functions on Rd. Among several variants, one simple statement is as follows:[50]
- If ƒ : H → R is a convex continuous function such that ƒ(x) tends to +∞ when ||x|| tends to ∞, then ƒ admits a minimum at some point x0 ∈ H.
[edit] Banach space properties
Any general property of Banach spaces continues to hold for Hilbert spaces. The open mapping theorem states that a continuous surjective linear transformation from one Banach space to another is an open mapping meaning that it sends open sets to open sets. A corollary is the bounded inverse theorem, that a continuous and bijective linear function from one Banach space to another is an isomorphism (that is, a continuous linear map whose inverse is also continuous). This theorem is considerably simpler to prove in the case of Hilbert spaces than in general Banach spaces.[51] The open mapping theorem is equivalent to the closed graph theorem, which asserts that a function from one Banach space to another is continuous if and only if its graph is a closed set.[52] In the case of Hilbert spaces, this is basic in the study of unbounded operators (see closed operator).The (geometrical) Hahn–Banach theorem asserts that a closed convex set can be separated from any point outside it by means of a hyperplane of the Hilbert space. This is an immediate consequence of the best approximation property: if y is the element of a closed convex set F closest to x, then the separating hyperplane is the plane perpendicular to the segment xy passing through its midpoint.[53]
[edit] Operators on Hilbert spaces
[edit] Bounded operators
The continuous linear operators A : H1 → H2 from a Hilbert space H1 to a second Hilbert space H2 are bounded in the sense that they map bounded sets to bounded sets. Conversely, if an operator is bounded, then it is continuous. The space of such bounded linear operators has a norm, the operator norm given byThe set B(H) of all bounded linear operators on H, together with the addition and composition operations, the norm and the adjoint operation, is a C*-algebra, which is a type of operator algebra.
An element A of B(H) is called self-adjoint or Hermitian if A∗ = A. If A is Hermitian and 〈Ax, x〉 ≥ 0 for every x, then A is called non-negative, written A ≥ 0; if equality holds only when x = 0, then A is called positive. The set of self adjoint operators admits a partial order, in which A ≥ B if A − B ≥ 0. If A has the form B∗B for some B, then A is non-negative; if B is invertible, then A is positive. A converse is also true in the sense that, for a non-negative operator A, there exists a unique non-negative square root B such that
An element U of B(H) is called unitary if U is invertible and its inverse is given by U∗. This can also be expressed by requiring that U be onto and〈Ux, Uy〉 =〈x, y〉 for all x and y in H. The unitary operators form a group under composition, which is the isometry group of H.
An element of B(H) is compact if it sends bounded sets to relatively compact sets. Equivalently, a bounded operator T is compact if, for any bounded sequence {xk}, the sequence {Txk} has a convergent subsequence. Many integral operators are compact, and in fact define a special class of operators known as Hilbert–Schmidt operators that are especially important in the study of integral equations. Fredholm operators are those which differ from a compact operator by a multiple of the identity, and are equivalently characterized as operators with a finite dimensional kernel and cokernel. The index of a Fredholm operator T is defined by
[edit] Unbounded operators
Unbounded operators are also tractable in Hilbert spaces, and have important applications to quantum mechanics.[54] An unbounded operator T on a Hilbert space H is defined to be a linear operator whose domain D(T) is a linear subspace of H. Often the domain D(T) is a dense subspace of H, in which case T is known as a densely-defined operator.The adjoint of a densely defined unbounded operator is defined in essentially the same manner as for bounded operators. Self-adjoint unbounded operators play the role of the observables in the mathematical formulation of quantum mechanics. Examples of self-adjoint unbounded operators on the Hilbert space L2(R) are:[55]
- A suitable extension of the differential operator
- where i is the imaginary unit and f is a differentiable function of compact support.
- The multiplication-by-x operator:
[edit] Constructions
[edit] Direct sums
Two Hilbert spaces H1 and H2 can be combined into another Hilbert space, called the (orthogonal) direct sum,[56] and denoted[edit] Tensor products
- Main article: Tensor product of Hilbert spaces
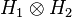 . The Hilbertian tensor product of H1 and H2, sometimes denoted by
. The Hilbertian tensor product of H1 and H2, sometimes denoted by 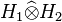 , is the Hilbert space obtained by completing
, is the Hilbert space obtained by completing 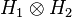 for the metric associated to this inner product.[57]
for the metric associated to this inner product.[57]An example is provided by the Hilbert space L2([0, 1]). The Hilbertian tensor product of two copies of L2([0, 1]) is isometrically and linearly isomorphic to the space L2([0, 1]2) of square-integrable functions on the square [0, 1]2. This isomorphism sends a simple tensor
 to the function
to the functionThis example is typical in the following sense.[58] Associated to every simple tensor product
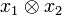 is the rank one operator
is the rank one operator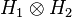 and the space of finite rank operators from H1∗ to H2. This extends to a linear isometry of the Hilbertian tensor product
and the space of finite rank operators from H1∗ to H2. This extends to a linear isometry of the Hilbertian tensor product 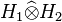 with the Hilbert space HS(H1∗, H2) of Hilbert-Schmidt operators from H1∗ to H2.
with the Hilbert space HS(H1∗, H2) of Hilbert-Schmidt operators from H1∗ to H2.[edit] Orthonormal bases
The notion of an orthonormal basis from linear algebra generalizes over to the case of Hilbert spaces.[59] In a Hilbert space H, an orthonormal basis is a family {ek}k ∈ B of elements of H satisfying the conditions:- Orthogonality: Every two different elements of B are orthogonal: 〈ek, ej〉= 0 for all k, j in B with k ≠ j.
- Normalization: Every element of the family has norm 1:||ek|| = 1 for all k in B.
- Completeness: The linear span of the family ek, k ∈ B, is dense in H.
- if 〈v, ek〉 = 0 for all k ∈ B and some v ∈ H then v = 0.
Examples of orthonormal bases include:
- the set {(1,0,0), (0,1,0), (0,0,1)} forms an orthonormal basis of R3 with the dot product;
- the sequence {ƒn : n ∈ Z} with ƒn(x) = exp(2πinx) forms an orthonormal basis of the complex space L2([0,1]);
[edit] Sequence spaces
The space ℓ 2 of square-summable sequences of complex numbers is the set of infinite sequencesAn orthonormal basis of ℓ 2(B) is indexed by the set B, given by
[edit] Bessel's inequality and Parseval's formula
Let ƒ1, …, ƒn be a finite orthonormal system in H. For an arbitrary vector x in H, letGeometrically, Bessel's inequality implies that the orthogonal projection of x onto the linear subspace spanned by the fi has norm that does not exceed that of x. In two dimensions, this is the assertion that the length of the leg of a right triangle may not exceed the length of the hypotenuse.
Bessel's inequality is a stepping stone to the more powerful Parseval identity which governs the case when Bessel's inequality is actually an equality. If {ek}k ∈ B is an orthonormal basis of H, then every element x of H may be written as
[edit] Hilbert dimension
As a consequence of Zorn's lemma, every Hilbert space admits an orthonormal basis; furthermore, any two orthonormal bases of the same space have the same cardinality, called the Hilbert dimension of the space.[61] For instance, since ℓ2(B) has an orthonormal basis indexed by B, its Hilbert dimension is the cardinality of B (which may be a finite integer, or a countable or uncountable cardinal number).As a consequence of Parseval's identity, if {ek}k ∈ B is an orthonormal basis of H, then the map Φ : H → ℓ2(B) defined by Φ(x) = (〈x,ek〉)k∈B is an isometric isomorphism of Hilbert spaces: it is a bijective linear mapping such that
[edit] Separable spaces
A Hilbert space is separable if and only if it admits a countable orthonormal basis. All infinite-dimensional separable Hilbert spaces are therefore isometrically isomorphic to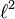 .
.In the past, Hilbert spaces were often required to be separable as part of the definition.[62] Most spaces used in physics are separable, and since these are all isomorphic to each other, one often refers to any infinite-dimensional separable Hilbert space as "the Hilbert space" or just "Hilbert space".[63] Even in quantum field theory, most of the Hilbert spaces are in fact separable, as stipulated by the Wightman axioms. However, it is sometimes argued that non-separable Hilbert spaces are also important in quantum field theory, roughly because the systems in the theory possess an infinite number of degrees of freedom and any infinite Hilbert tensor product (of spaces of dimension greater than one) is non-separable.[64] For instance, a bosonic field can be naturally thought of as an element of a tensor product whose factors represent harmonic oscillators at each point of space. From this perspective, the natural state space of a boson might seem to be a non-separable space.[64] However, it is only a small separable subspace of the full tensor product that can contain physically meaningful fields (on which the observables can be defined). Another non-separable Hilbert space models the state of an infinite collection of particles in an unbounded region of space. An orthonormal basis of the space is indexed by the density of the particles, a continuous parameter, and since the set of possible densities is uncountable, the basis is not countable.[64]
[edit] Orthogonal complements and projections
If S is a subset of a Hilbert space H, the set of vectors orthogonal to S is defined byThe linear operator PV : H → H which maps x to v is called the orthogonal projection onto V. There is a natural one-to-one correspondence between the set of all closed subspaces of H and the set of all bounded self-adjoint operators P such that P2 = P. Specifically,
- Theorem. The orthogonal projection PV is a self-adjoint linear operator on H of norm ≤ 1 with the property P2V = PV. Moreover, any self-adjoint linear operator E such that E2 = E is of the form PV, where V is the range of E. For every x in H, PV(x) is the unique element v of V which minimizes the distance ||x − v||.
An operator P such that P = P2 = P∗ is called an orthogonal projection. The orthogonal projection PV onto a closed subspace V of H is the adjoint of the inclusion mapping
The operator norm of a projection P onto a non-zero closed subspace is equal to one:
- A Banach space of dimension higher than 2 is (isometrically) a Hilbert space if and only if, to every closed subspace V, there is an operator PV of norm one whose image is V such that

- A Banach space X is topologically and linearly isomorphic to a Hilbert space if and only if, to every closed subspace V, there is a closed subspace W such that X is equal to the internal direct sum
 .
.
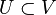 , then
, then  with equality holding if and only if V is contained in the closure of U. This result is a special case of the Hahn–Banach theorem. The closure of a subspace can be completely characterized in terms of the orthogonal complement: If V is a subspace of H, then the closure of V is equal to
with equality holding if and only if V is contained in the closure of U. This result is a special case of the Hahn–Banach theorem. The closure of a subspace can be completely characterized in terms of the orthogonal complement: If V is a subspace of H, then the closure of V is equal to  . The orthogonal complement is thus a Galois connection on the partial order of subspaces of a Hilbert space. In general, the orthogonal complement of a sum of subspaces is the intersection of the orthogonal complements:[68]
. The orthogonal complement is thus a Galois connection on the partial order of subspaces of a Hilbert space. In general, the orthogonal complement of a sum of subspaces is the intersection of the orthogonal complements:[68]  . If the Vi are in addition closed, then
. If the Vi are in addition closed, then  .
.[edit] Spectral theory
There is a well-developed spectral theory for self-adjoint operators in a Hilbert space, that is roughly analogous to the study of symmetric matrices over the reals or self-adjoint matrices over the complex numbers.[69] In the same sense, one can obtain a "diagonalization" of a self-adjoint operator as a suitable sum (actually an integral) of orthogonal projection operators.The spectrum of an operator T, denoted σ(T) is the set of complex numbers λ such that T − λ lacks a continuous inverse. If T is bounded, then the spectrum is always a compact set in the complex plane, and lies inside the disc
 If T is self-adjoint, then the spectrum is real. In fact, it is contained in the interval [m,M] where
If T is self-adjoint, then the spectrum is real. In fact, it is contained in the interval [m,M] whereThe eigenspaces of an operator T are given by
However, the spectral theorem of a self-adjoint operator T takes a particularly simple form if, in addition, T is assumed to be a compact operator. The spectral theorem for compact self-adjoint operators states:[70]
- A compact self-adjoint operator T has only countably (or finitely) many spectral values. The spectrum of T has no limit point in the complex plane except possibly zero. The eigenspaces of T decompose H into an orthogonal direct sum:
- Moreover, if Eλ denotes the orthogonal projection onto the eigenspace Hλ, then
- where the sum converges with respect to the norm on B(H).
The general spectral theorem for self-adjoint operators involves a kind of operator-valued Riemann–Stieltjes integral, rather than an infinite summation.[71] The spectral family associated to T associates to each real number λ an operator Eλ, which is the projection onto the nullspace of the operator (T − λ) + , where the positive part of a self-adjoint operator is defined by
A major application of spectral methods is the spectral mapping theorem, which allows one to apply to a self-adjoint operator T any continuous complex function ƒ defined on the spectrum of T by forming the integral
The spectral theory of unbounded self-adjoint operators is only marginally more difficult than for bounded operators. The spectrum of an unbounded operator is defined in precisely the same way as for bounded operators: λ is a spectral value if the resolvent operator
- Rλ = (T − λ) − 1
A precise version of the spectral theorem which holds in this case is:[73]
- Given a densely-defined self-adjoint operator T on a Hilbert space H, there corresponds a unique resolution of the identity E on the Borel sets of R, such that
- for all x ∈ D(T) and y ∈ H. The spectral measure E is concentrated on the spectrum of T.
literally copied from : http://en.wikipedia.org/wiki/Hilbert_space
Subscribe to:
Comments (Atom)






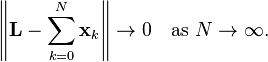





























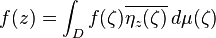


![-\frac{d}{dx}\left[p(x)\frac{dy}{ dx}\right]+q(x)y=\lambda w(x)y](http://upload.wikimedia.org/math/4/6/8/46843bd5250780c5b80f9ce7cedb4a94.png)