The
mathematical concept of a
Hilbert space, named after
David Hilbert, generalizes the notion of
Euclidean space. It extends the methods of
vector algebra and
calculus from the two-dimensional
Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions. A Hilbert space is an abstract
vector space possessing the
structure of an
inner product that allows length and angle to be measured. Furthermore, Hilbert spaces are required to be
complete, a property that stipulates the existence of enough
limits in the space to allow the techniques of calculus to be used.
Hilbert spaces arise naturally and frequently in
mathematics,
physics, and
engineering, typically as infinite-dimensional
function spaces. The earliest Hilbert spaces were studied from this point of view in the first decade of the 20th century by
David Hilbert,
Erhard Schmidt, and
Frigyes Riesz. They are indispensable tools in the theories of
partial differential equations,
quantum mechanics,
Fourier analysis (which includes applications to
signal processing and heat transfer) and
ergodic theory which forms the mathematical underpinning of the study of
thermodynamics.
John von Neumann coined the term "Hilbert space" for the abstract concept underlying many of these diverse applications. The success of Hilbert space methods ushered in a very fruitful era for
functional analysis. Apart from the classical Euclidean spaces, examples of Hilbert spaces include
spaces of square-integrable functions,
spaces of sequences,
Sobolev spaces consisting of
generalized functions, and
Hardy spaces of
holomorphic functions.
Geometric intuition plays an important role in many aspects of Hilbert space theory. Exact analogs of the
Pythagorean theorem and
parallelogram law hold in a Hilbert space. At a deeper level, perpendicular projection onto a subspace (the analog of "
dropping the altitude" of a triangle) plays a significant role in optimization problems and other aspects of the theory. An element of a Hilbert space can be uniquely specified by its coordinates with respect to a set of
coordinate axes (an
orthonormal basis), in analogy with Cartesian coordinates in the plane. When that set of axes is
countably infinite, this means that the Hilbert space can also usefully be thought of in terms of
infinite sequences that are
square-summable.
Linear operators on a Hilbert space are likewise fairly concrete objects: in good cases, they are simply transformations that stretch the space by different factors in mutually perpendicular directions in a sense that is made precise by the study of their
spectrum.
[edit] Definition and illustration
[edit] Motivating example: Euclidean space
One of the most familiar examples of a Hilbert space is the
Euclidean space consisting of three-dimensional
vectors, denoted by
R3, and equipped with the
dot product. The dot product takes two vectors
x and
y, and produces a real number
x·
y. If
x and
y are represented in
Cartesian coordinates, then the dot product is defined by

The dot product satisfies the properties:
- It is symmetric in x and y: x·y = y·x.
- It is linear in its first argument: (ax1 + bx2)·y = ax1·y + bx2·y for any scalars a, b, and vectors x1, x2, and y.
- It is positive definite: for all vectors x, x·x ≥ 0 with equality if and only if x = 0.
An operation on pairs of vectors that, like the dot product, satisfies these three properties is known as a (real)
inner product. A
vector space equipped with such an inner product is known as a (real)
inner product space. Every finite-dimensional inner product space is also a Hilbert space. The basic feature of the dot product that connects it with Euclidean geometry is that it is related to both the length (or
norm) of a vector, denoted ||
x||, and to the angle θ between two vectors
x and
y by means of the formula


Completeness means that if a particle moves along the broken path (in blue) travelling a finite total distance, then the particle has a well-defined net displacement (in orange).
in Euclidean space relies on the ability to compute
limits, and to have useful criteria for concluding that limits exist. A
mathematical series

consisting of vectors in
R3 is
absolutely convergent provided that the sum of the lengths converges as an ordinary series of real numbers:
[1]

Just as with a series of scalars, a series of vectors that converges absolutely also converges to some limit vector
L in the Euclidean space, in the sense that
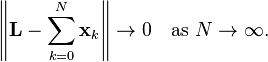
This property expresses the
completeness of Euclidean space: that a series which converges absolutely also converges in the ordinary sense.
[edit] Definition
A
Hilbert space H is a
real or
complex inner product space that is also a
complete metric space with respect to the distance function induced by the inner product.
[2] To say that
H is a complex inner product space means that
H is a complex vector space on which there is an inner product 〈
x,
y〉 associating a complex number to each pair of elements
x,
y of
H that satisfies the following properties:
-

- 〈x,y〉 is linear in its first argument.[3] For all complex numbers a and b,
-

-

- where the case of equality holds precisely when x = 0.
It follows from properties 1 and 2 that a complex inner product is antilinear in its second argument, meaning that

A real inner product space is defined in the same way, except that
H is a real vector space and the inner product takes real values. Such an inner product will be bilinear: that is, linear in each argument.
The
norm defined by the inner product 〈•,•〉 is the real-valued function

and the distance between two points
x,
y in
H is defined in terms of the norm by

That this function is a distance function means (1) that it is symmetric in
x and
y, (2) that the distance between
x and itself is zero, and otherwise the distance between
x and
y must be positive, and (3) that the
triangle inequality holds, meaning that the length of one leg of a triangle
xyz cannot exceed the sum of the lengths of the other two legs:

This last property is ultimately a consequence of the more fundamental
Cauchy–Schwarz inequality, which asserts

with equality if and only if
x and
y are
linearly dependent.
Relative to a distance function defined in this way, any inner product space is a
metric space, and sometimes is known as a
pre-Hilbert space.
[4] A pre-Hilbert space is a Hilbert space if in addition it is complete. Completeness is expressed using a form of the
Cauchy criterion for sequences in
H: a pre-Hilbert space
H is
complete if every
Cauchy sequence converges with respect to this norm to an element in the space. Completeness can be characterized by the following equivalent condition: if a series of vectors
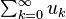 converges absolutely
converges absolutely in the sense that

then the series converges in
H, in the sense that the partial sums converge to an element of
H.
As a complete normed space, Hilbert spaces are by definition also
Banach spaces. As such they are
topological vector spaces, in which
topological notions like the
openness and
closedness of subsets are well-defined. Of special importance is the notion of a closed
linear subspace of a Hilbert space which, with the inner product induced by restriction, is also complete (being a closed set in a complete metric space) and therefore a Hilbert space in its own right.
[edit] Second example: sequence spaces
The
sequence space ℓ2 consists of all
infinite sequences z = (
z1,
z2,...) of complex numbers such that the
series

converges. The inner product on
ℓ2 is defined by

with the latter series converging as a consequence of the Cauchy–Schwarz inequality.
Completeness of the space holds provided that whenever a series of elements from
ℓ2 converges absolutely (in norm), then it converges to an element of
ℓ2. The proof is basic in
mathematical analysis, and permits mathematical series of elements of the space to be manipulated with the same ease as series of complex numbers (or vectors in a finite-dimensional Euclidean space).
[5]
[edit] History
Prior to the development of Hilbert spaces, other generalizations of Euclidean spaces were known to mathematicians and physicists. In particular, the idea of an
abstract linear space had gained some traction towards the end of the 19th century:
[6] this is a space whose elements can be added together and multiplied by scalars (such as
real or
complex numbers) without necessarily identifying these elements with
"geometric" vectors, such as position and momentum vectors in physical systems. Other objects studied by mathematicians at the turn of the 20th century, in particular spaces of
sequences (including
series) and spaces of functions,
[7] can naturally be thought of as linear spaces. Functions, for instance, can be added together or multiplied by constant scalars, and these operations obey the algebraic laws satisfied by addition and scalar multiplication of spatial vectors.
In the first decade of the 20th century, parallel developments led to the introduction of Hilbert spaces. The first of these was the observation, which arose during
David Hilbert and
Erhard Schmidt's study of
integral equations,
[8] that two
square-integrable real-valued functions
f and
g on an interval [
a,
b] have an
inner product

which has many of the familiar properties of the Euclidean dot product. In particular, the idea of an
orthogonal family of functions has meaning. Schmidt exploited the similarity of this inner product with the usual dot product to prove an analog of the
spectral decomposition for an operator of the form

where
K is a continuous function symmetric in
x and
y. The resulting
eigenfunction expansion expresses the function
K as a series of the form

where the functions
φn are orthogonal in the sense that
〈φn,φm〉 = 0 for all
n ≠ m. The individual terms in this series are sometimes referred to as elementary product solutions. However, there are eigenfunction expansions which fail to converge in a suitable sense to a square-integrable function: the missing ingredient, which ensures convergence, is completeness.
[9]
The second development was the
Lebesgue integral, an alternative to the
Riemann integral introduced by
Henri Lebesgue in 1904.
[10] The Lebesgue integral made it possible to integrate a much broader class of functions. In 1907,
Frigyes Riesz and
Ernst Sigismund Fischer independently proved that the space
L2 of square Lebesgue-integrable functions is a
complete metric space.
[11] As a consequence of the interplay between geometry and completeness, the 19th century results of
Joseph Fourier,
Friedrich Bessel and
Marc-Antoine Parseval on
trigonometric series easily carried over to these more general spaces, resulting in a geometrical and analytical apparatus now usually known as the
Riesz-Fischer theorem.
[12]
Further basic results were proved in the early 20th century. For example, the
Riesz representation theorem was independently established by
Maurice Fréchet and
Frigyes Riesz in 1907.
[13] John von Neumann coined the term
abstract Hilbert space in his work on unbounded
Hermitian operators.
[14] Although other mathematicians such as
Hermann Weyl and
Norbert Wiener had already studied particular Hilbert spaces in great detail, often from a physically-motivated point of view, von Neumann gave the first complete and axiomatic treatment of them.
[15] Von Neumann later used them in his seminal work on the foundations of quantum mechanics,
[16] and in his continued work with
Eugene Wigner. The name "Hilbert space" was soon adopted by others, for example by Hermann Weyl in his book on quantum mechanics and the theory of groups.
[17]
The significance of the concept of a Hilbert space was underlined with the realization that it offers one of the best
mathematical formulations of quantum mechanics.
[18] In short, the states of a quantum mechanical system are vectors in a certain Hilbert space, the observables are
hermitian operators on that space, the
symmetries of the system are
unitary operators, and
measurements are
orthogonal projections. The relation between quantum mechanical symmetries and unitary operators provided an impetus for the development of the
unitary representation theory of
groups, initiated in the 1928 work of Hermann Weyl.
[17] On the other hand, in the early 1930s it became clear that certain properties of classical
dynamical systems can be analyzed using Hilbert space techniques in the framework of
ergodic theory.
[19]
The algebra of
observables in quantum mechanics is naturally an algebra of operators defined on a Hilbert space, according to
Werner Heisenberg's
matrix mechanics formulation of quantum theory. Von Neumann began investigating
operator algebras in the 1930s, as
rings of operators on a Hilbert space. The kind of algebras studied by von Neumann and his contemporaries are now known as
von Neumann algebras. In the 1940s,
Israel Gelfand,
Mark Naimark and
Irving Segal gave a definition of a kind of operator algebras called
C*-algebras that on the one hand made no reference to an underlying Hilbert space, and on the other extrapolated many of the useful features of the operator algebras that had previously been studied. The spectral theorem for self-adjoint operators in particular that underlies much of the existing Hilbert space theory was generalized to C*-algebras. These techniques are now basic in abstract harmonic analysis and representation theory.
[edit] Examples
[edit] Lebesgue spaces
Lebesgue spaces are
function spaces associated to
measure spaces (
X,
M,
μ), where
X is a set,
M is a
σ-algebra of subsets of
X, and
μ is a
countably additive measure on
M. Let
L2(
X,μ) be the space of those complex-valued measurable functions on
X for which the
Lebesgue integral of the square of the
absolute value of the function is finite, i.e., for a function
f in
L2(
X,μ),

and where functions are identified if and only if they differ only on a
set of measure zero.
The inner product of functions
f and
g in
L2(
X,μ) is then defined as

For
f and
g in
L2, this integral exists because of the Cauchy–Schwarz inequality, and defines an inner product on the space. Equipped with this inner product,
L2 is in fact complete.
[20] The Lebesgue integral is essential to ensure completeness: on domains of real numbers, for instance, not enough functions are
Riemann integrable.
[21]
The Lebesgue spaces appear in many natural settings. The spaces
L2(
R) and
L2([0,1]) of square-integrable functions with respect to the
Lebesgue measure on the real line and unit interval, respectively, are natural domains on which to define the Fourier transform and Fourier series. In other situations, the measure may be something other than the ordinary Lebesgue measure on the real line. For instance, if
w is any positive measurable function, the space of all measurable functions
f on the interval [0,1] satisfying

is called the
weighted L2 space L2
w([0,1]), and
w is called the weight function. The inner product is defined by

The weighted space
L2
w([0,1]) is identical with the Hilbert space
L2([0,1],μ) where the measure μ of a Lebesgue-measurable set
A is defined by

Weighted
L2 spaces like this are frequently used to study orthogonal polynomials, because different families of orthogonal polynomials are orthogonal with respect to different weighting functions.
[edit] Sobolev spaces
Sobolev spaces, denoted by
Hs or
W s, 2, are Hilbert spaces. These are a special kind of
function space in which
differentiation may be performed, but which (unlike other
Banach spaces such as the
Hölder spaces) support the structure of an inner product. Because differentiation is permitted, Sobolev spaces are a convenient setting for the theory of
partial differential equations.
[22] They also form the basis of the theory of
direct methods in the calculus of variations.
[23]
For
s a non-negative integer and
Ω ⊂ Rn, the Sobolev space
Hs(Ω) contains L
2 functions whose
weak derivatives of order up to
s are also L
2. The inner product in
Hs(Ω) is

where the dot indicates the dot product in the Euclidean space of partial derivatives of each order. Sobolev spaces can also be defined when
s is not an integer.
Sobolev spaces are also studied from the point of view of spectral theory, relying more specifically on the Hilbert space structure. If Ω is a suitable domain, then one can define the Sobolev space
Hs(Ω) as the space of
Bessel potentials;
[24] roughly,

Here Δ is the Laplacian and (1 − Δ)
−s/2 is understood in terms of the
spectral mapping theorem. Apart from providing a workable definition of Sobolev spaces for non-integer
s, this definition also has particularly desirable properties under the
Fourier transform that make it ideal for the study of
pseudodifferential operators. Using these methods on a
compact Riemannian manifold, one can obtain for instance the
Hodge decomposition which is the basis of
Hodge theory.
[25]
[edit] Spaces of holomorphic functions
- Hardy spaces
The
Hardy spaces are function spaces, arising in
complex analysis and
harmonic analysis, whose elements are certain
holomorphic functions in a complex domain.
[26] Let
U denote the
unit disc in the complex plane. Then the Hardy space
H2(
U) is defined to be the space of holomorphic functions
f on
U such that the means

remain bounded for
r < 1. The norm on this Hardy space is defined by

Hardy spaces in the disc are related to Fourier series. A function
f is in
H2(
U) if and only if

where

Thus
H2(
U) consists of those functions which are L
2 on the circle, and whose negative frequency Fourier coefficients vanish.
- Bergman spaces
The
Bergman spaces are another family of Hilbert spaces of holomorphic functions.
[27] Let
D be a bounded open set in the
complex plane (or a higher dimensional complex space) and let
L2,h(
D) be the space of holomorphic functions
ƒ in
D that are also in
L2(
D) in the sense that

where the integral is taken with respect to the Lebesgue measure in
D. Clearly
L2,h(
D) is a subspace of
L2(
D); in fact, it is a
closed subspace, and so a Hilbert space in its own right. This is a consequence of the estimate, valid on
compact subsets
K of
D, that

which in turn follows from
Cauchy's integral formula. Thus convergence of a sequence of holomorphic functions in
L2(
D) implies also
compact convergence, and so the limit function is also holomorphic. Another consequence of this inequality is that the linear functional that evaluates a function
ƒ at a point of
D is actually continuous on
L2,h(
D). The Riesz representation theorem implies that the evaluation functional can be represented as an element of
L2,h(
D). Thus, for every
z ∈
D, there is a function η
z ∈
L2,h(
D) such that
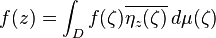
for all
ƒ ∈
L2,h(
D). The integrand

is known as the
Bergman kernel of
D. This
integral kernel satisfies a reproducing property

A Bergman space is an example of a
reproducing kernel Hilbert space, which is a Hilbert space of functions along with a kernel
K(ζ,
z) that verifies a reproducing property analogous to this one. The Hardy space
H2(
D) also admits a reproducing kernel, known as the
Szegő kernel.
[28] Reproducing kernels are common in other areas of mathematics as well. For instance, in
harmonic analysis the
Poisson kernel is a reproducing kernel for the Hilbert space of square-integrable
harmonic functions in the
unit ball. That the latter is a Hilbert space at all is a consequence of the mean value theorem for harmonic functions.
[edit] Applications
Many of the applications of Hilbert spaces exploit the fact that Hilbert spaces support generalizations of simple geometric concepts like
projection and
change of basis from their usual finite dimensional setting. In particular, the
spectral theory of
continuous self-adjoint linear operators on a Hilbert space generalizes the usual
spectral decomposition of a
matrix, and this often plays a major role in applications of the theory to other areas of mathematics and physics.
[edit] Sturm–Liouville theory
In the theory of
ordinary differential equations, spectral methods on a suitable Hilbert space are used to study the behavior of eigenvalues and eigenfunctions of differential equations. For example, the
Sturm–Liouville problem arises in the study of the harmonics of waves in a violin string or a drum, and is a central problem in
ordinary differential equations.
[29] The problem is a differential equation of the form
![-\frac{d}{dx}\left[p(x)\frac{dy}{ dx}\right]+q(x)y=\lambda w(x)y](http://upload.wikimedia.org/math/4/6/8/46843bd5250780c5b80f9ce7cedb4a94.png)
for an unknown function
y on an interval [
a,
b], satisfying general homogeneous
Robin boundary conditions

The functions
p,
q, and
w are given in advance, and the problem is to find the function
y and constants λ for which the equation has a solution. The problem only has solutions for certain values of λ, called eigenvalues of the system, and this is a consequence of the spectral theorem for
compact operators applied to the
integral operator defined by the
Green's function for the system. Furthermore, another consequence of this general result is that the eigenvalues λ of the system can be arranged in an increasing sequence tending to infinity.
[30]
[edit] Partial differential equations
Hilbert spaces form a basic tool in the study of
partial differential equations.
[22] For many classes of partial differential equations, such as linear
elliptic equations, it is possible to consider a generalized solution (known as a
weak solution) by enlarging the class of functions. Many weak formulations involve the class of
Sobolev functions, which is a Hilbert space. A suitable weak formulation reduces to a geometrical problem the analytic problem of finding a solution or, often what is more important, showing that a solution exists and is unique for given boundary data. For linear elliptic equations, one geometrical result that ensures unique solvability for a large class of problems is the
Lax–Milgram theorem. This strategy forms the rudiment of the
Galerkin method (a
finite element method) for numerical solution of partial differential equations.
[31]
A typical example is the
Poisson equation −Δu = g with
Dirichlet boundary conditions in a bounded domain Ω in
R2. The weak formulation consists of finding a function
u such that, for all continuously differentiable functions
v in Ω vanishing on the boundary:

This can be recast in terms of the Hilbert space
H1
0(Ω) consisting of functions
u such that
u, along with its weak partial derivatives, are square integrable on Ω, and which vanish on the boundary. The question then reduces to finding
u in this space such that for all
v in this space
- a(u,v) = b(v)
where
a is a continuous
bilinear form, and
b is a continuous
linear functional, given respectively by

Since the Poisson equation is
elliptic, it follows from Poincaré's inequality that the bilinear form
a is
coercive. The Lax-Milgram theorem then ensures the existence and uniqueness of solutions of this equation.
Hilbert spaces allow for many elliptic partial differential equations to be formulated in a similar way, and the Lax-Milgram theorem is then a basic tool in their analysis. With suitable modifications, similar techniques can be applied to
parabolic partial differential equations and certain
hyperbolic partial differential equations.
[edit] Ergodic theory
The field of
ergodic theory is the study of the long-term behavior of
chaotic dynamical systems. The protypical case of a field to which ergodic theory is applicable is that of
thermodynamics in which, although the microscopic state of a system is extremely complicated—it is impossible to understand the ensemble of individual collisions between particles of matter—the average behavior over sufficiently long time intervals is tractable. The
laws of thermodynamics are assertions about such average behavior. In particular, one formulation of the
zeroth law of thermodynamics asserts that over sufficiently long timescales, the only functionally independent measurement that one can make of a thermodynamic system in equilibrium is its total energy, in the form of
temperature.
An ergodic dynamical system is one for which, apart from the energy—measured by the
Hamiltonian—there are no other functionally independent
conserved quantities on the
phase space. More explicitly, suppose that the energy
E is fixed, and let Ω
E be the subset of the phase space consisting of all states of energy
E (an energy surface), and let
Tt denote the evolution operator on the phase space. The dynamical system is ergodic if there are no continuous non-constant functions on Ω
E such that

for all
w on Ω
E and all time
t.
Liouville's theorem implies that there exists a
measure μ on the energy surface that is invariant under the time translation. As a result, time translation is a
unitary transformation of the Hilbert space
L2(Ω
E,μ) consisting of square-integrable functions on the energy surface Ω
E with respect to the inner product

The von Neumann mean ergodic theorem
[19] states the following:
- If Ut is a (strongly continuous) one-parameter semigroup of unitary operators on a Hilbert space H, and P is the orthogonal projection onto the space of common fixed points of Ut, {x∈H | Utx = x for all t > 0}, then
-

For an ergodic system, the fixed set of the time evolution consists only of the constant functions, so the ergodic theorem implies the following:
[32] for any function
ƒ ∈
L2(Ω
E,μ),

That is, the long time average of an observable
ƒ is equal to its expectation value over an energy surface.
[edit] Fourier analysis
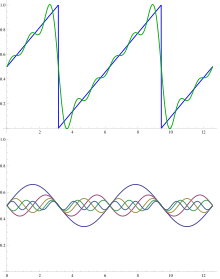
Superposition of sinusoidal wave basis functions (bottom) to form a sawtooth wave (top)

Spherical harmonics, an orthonormal basis for the Hilbert space of square-integrable functions on the sphere, shown graphed along the radial direction
One of the basic goals of
Fourier analysis is to decompose a function into a (possibly infinite)
linear combination of given basis functions: the associated
Fourier series. The classical Fourier series associated to a function
ƒ defined on the interval [0,1] is a series of the form

where

The example of adding up the first few terms in a Fourier series for a sawtooth function is shown in the figure. The basis functions are sine waves with wavelengths λ/
n (
n=integer) shorter than the wavelength λ of the sawtooth itself (except for
n=1, the
fundamental wave). All basis functions have nodes at the nodes of the sawtooth, but all but the fundamental have additional nodes. The oscillation of the summed terms about the sawtooth is called the
Gibbs phenomenon.
A significant problem in classical Fourier series asks in what sense the Fourier series converges, if at all, to the function
ƒ. Hilbert space methods provide one possible answer to this question.
[33] The functions
en(θ) = e
2πinθ form an orthogonal basis of the Hilbert space L
2([0,1]). Consequently, any square-integrable function can be expressed as a series

and, moreover, this series converges in the Hilbert space sense (that is, in the
L2 mean).
The problem can also be studied from the abstract point of view: every Hilbert space has an
orthonormal basis, and every element of the Hilbert space can be written in a unique way as a sum of multiples of these basis elements. The coefficients appearing on these basis elements are sometimes known abstractly as the Fourier coefficients of the element of the space.
[34] The abstraction is especially useful when it is more natural to use different basis functions for a space such as
L2([0,1]). In many circumstances, it is desirable not to decompose a function into trigonometric functions, but rather into
orthogonal polynomials or
wavelets for instance,
[35] and in higher dimensions into
spherical harmonics.
[36]
For instance, if
en are any orthonormal basis functions of
L2[0,1], then a given function in
L2[0,1] can be approximated as a finite linear combination
[37]

The coefficients {
aj} are selected to make the magnitude of the difference ||
ƒ − ƒn||
2 as small as possible. Geometrically, the
best approximation is the
orthogonal projection of
ƒ onto the subspace consisting of all linear combinations of the {
ej}, and can be calculated by
[38]

That this formula minimizes the difference ||
ƒ − ƒn||
2 is a consequence of
Bessel's inequality and Parseval's formula.
In various applications to physical problems, a function can be decomposed into physically meaningful
eigenfunctions of a
differential operator (typically the
Laplace operator): this forms the foundation for the spectral study of functions, in reference to the
spectrum of the differential operator.
[39] A concrete physical application involves the problem of
hearing the shape of a drum: given the fundamental modes of vibration that a drumhead is capable of producing, can one infer the shape of the drum itself?
[40] The mathematical formulation of this question involves the
Dirichlet eigenvalues of the Laplace equation in the plane, that represent the fundamental modes of vibration in direct analogy with the integers that represent the fundamental modes of vibration of the violin string.
Spectral theory also underlies certain aspects of the
Fourier transform of a function. Whereas Fourier analysis decomposes a function defined on a
compact set into the discrete spectrum of the Laplacian (which corresponds to the vibrations of a violin string or drum), the Fourier transform of a function is the decomposition of a function defined on all of Euclidean space into its components in the
continuous spectrum of the Laplacian. The Fourier transformation is also geometrical, in a sense made precise by the
Plancherel theorem, that asserts that it is an
isometry of one Hilbert space (the "time domain") with another (the "frequency domain"). This isometry property of the Fourier transformation is a recurring theme in abstract
harmonic analysis, as evidenced for instance by the
Plancherel theorem for spherical functions occurring in
noncommutative harmonic analysis.
[edit] Quantum mechanics
In the mathematically rigorous formulation of quantum mechanics, developed by
Paul Dirac[41] and
John von Neumann[42], the possible states (more precisely, the
pure states) of a quantum mechanical system are represented by
unit vectors (called
state vectors) residing in a complex separable Hilbert space, known as the
state space, well defined up to a complex number of norm 1 (the phase factor). In other words, the possible states are points in the
projectivization of a Hilbert space, usually called the
complex projective space. The exact nature of this Hilbert space is dependent on the system; for example, the position and momentum states for a single non-relativistic spin zero particle is the space of all
square-integrable functions, while the states for the spin of a single proton are unit elements of the two-dimensional complex Hilbert space of
spinors. Each observable is represented by a
self-adjoint linear operator acting on the state space. Each eigenstate of an observable corresponds to an
eigenvector of the operator, and the associated
eigenvalue corresponds to the value of the observable in that eigenstate.
The time evolution of a quantum state is described by the
Schrödinger equation, in which the
Hamiltonian, the
operator corresponding to the
total energy of the system, generates time evolution.
The inner product between two state vectors is a complex number known as a
probability amplitude. During an ideal measurement of a quantum mechanical system, the probability that a system collapses from a given initial state to a particular eigenstate is given by the square of the
absolute value of the probability amplitudes between the initial and final states. The possible results of a measurement are the eigenvalues of the operator—which explains the choice of self-adjoint operators, for all the eigenvalues must be real. The probability distribution of an observable in a given state can be found by computing the spectral decomposition of the corresponding operator.
For a general system, states are typically not pure, but instead are represented as statistical mixtures of pure states, or mixed states, given by
density matrices: self-adjoint operators of
trace one on a Hilbert space. Moreover, for general quantum mechanical systems, the effects of a single measurement can influence other parts of a system in a manner that is described instead by a
positive operator valued measure. Thus the structure both of the states and observables in the general theory is considerably more complicated than the idealization for pure states.
Heisenberg's
uncertainty principle is represented by the statement that the operators corresponding to certain observables do not commute, and gives a specific form that the
commutator must have.
[edit] Properties
[edit] Pythagorean identity
Two vectors
u and
v in a Hilbert space
H are orthogonal when

= 0. The notation for this is
u ⊥ v. More generally, when
S is a subset in
H, the notation
u ⊥ S means that
u is orthogonal to every element from
S.
When
u and
v are orthogonal, one has
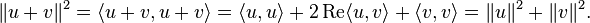
By induction on
n, this is extended to any family
u1,...,
un of
n orthogonal vectors,

Whereas the Pythagorean identity as stated is valid in any inner product space, completeness is required for the extension of the Pythagorean identity to series. A series Σ
uk of
orthogonal vectors converges in
H if and only if the series of squares of norms converges, and

Furthermore, the sum of a series of orthogonal vectors is independent of the order in which it is taken.
[edit] Parallelogram identity and polarization

Geometrically, the parallelogram identity asserts that
AC2 + BD2 = 2(AB2 + AD2). In words, the sum of the squares of the diagonals is twice the sum of the squares of any two adjacent sides.
By definition, every Hilbert space is also a
Banach space. Furthermore, in every Hilbert space the following
parallelogram identity holds:

Conversely, every Banach space in which the parallelogram identity holds is a Hilbert space, and the inner product is uniquely determined by the norm by the
polarization identity.
[43] For real Hilbert spaces, the polarization identity is
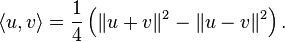
For complex Hilbert spaces, it is

The parallelogram law implies that any Hilbert space is a
uniformly convex Banach space.
[44]
[edit] Best approximation
If
C is a non-empty closed convex subset of a Hilbert space
H and
x a point in
H, there exists a unique point
y ∈
C which minimizes the distance between
x and points in
C,
[45]

This is equivalent to saying that there is a point with minimal norm in the translated convex set
D =
C − x. The proof consists in showing that every minimizing sequence (
dn) ⊂
D is Cauchy (using the parallelogram identity) hence converges (using completeness) to a point in
D that has minimal norm. More generally, this holds in any uniformly convex Banach space.
[46]
When this result is applied to a closed subspace
F of
H, it can be shown that the point
y ∈
F closest to
x is characterized by
[47]

This point
y is the
orthogonal projection of
x onto
F, and the mapping
PF :
x → y is linear (see
Orthogonal complements and projections). This result is especially significant in
applied mathematics, especially
numerical analysis, where it forms the basis of
least squares methods.
In particular, when
F is not equal to
H, one can find a non-zero vector
v orthogonal to
F (select
x not in
F and
v =
x − y). A very useful criterion is obtained by applying this observation to the closed subspace
F generated by a subset
S of
H.
- A subset S of H spans a dense vector subspace if (and only if) the vector 0 is the sole vector v ∈ H orthogonal to S.
[edit] Duality
The
dual space H∗ is the space of all
continuous linear functions from the space
H into the base field. It carries a natural norm, defined by

This norm satisfies the parallelogram law, and so the dual space is also an inner product space. The dual space is also complete, and so it is a Hilbert space in its own right.
The
Riesz representation theorem affords a convenient description of the dual. To every element
u of
H, there is a unique element
φu of
H∗, defined by
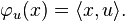
The mapping

is an antilinear mapping from
H to
H∗. The Riesz representation theorem states that this mapping is an antilinear isomorphism.
[48] Thus to every element
φ of the dual
H∗ there exists one and only one
uφ in
H such that

for all
x ∈
H. The inner product on the dual space
H∗ satisfies

The reversal of order on the right-hand side restores linearity in
φ from the antilinearity of
uφ. In the real case, the antilinear isomorphism from
H to its dual is actually an isomorphism, and so real Hilbert spaces are naturally isomorphic to their own duals.
The representing vector
uφ is obtained in the following way. When
φ ≠ 0, the
kernel F = ker
φ is a closed vector subspace of
H, not equal to
H, hence there exists a non-zero vector
v orthogonal to
F. The vector
u is a suitable scalar multiple
λv of
v. The requirement that
φ(
v) = 〈
v,
u〉 yields
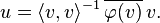
This correspondence
φ ↔
u is exploited by the
bra-ket notation popular in
physics. It is common in physics to assume that the inner product, denoted by 〈
x|
y〉, is linear on the right,

The result 〈
x|
y〉 can be seen as the action of the linear functional 〈
x| (the
bra) on the vector |
y〉 (the
ket).
The Riesz representation theorem relies fundamentally not just on the presence of an inner product, but also on the completeness of the space. In fact, the theorem implies that the
topological dual of any inner product space can be identified with its completion. An immediate consequence of the Riesz representation theorem is also that a Hilbert space
H is
reflexive, meaning that the natural map from
H into its
double dual space is an isomorphism.
[edit] Weakly convergent sequences
In a Hilbert space
H, a sequence {
xn} is
weakly convergent to a vector
x ∈
H when

for every
v ∈ H.
For example, any orthonormal sequence {
ƒn} converges weakly to 0, as a consequence of
Bessel's inequality. Every weakly convergent sequence {
xn} is bounded, by the
uniform boundedness principle.
Conversely, every bounded sequence in a Hilbert space admits weakly convergent subsequences (
Alaoglu's theorem).
[49] This fact may be used to prove minimization results for continuous
convex functionals, in the same way that the
Bolzano-Weierstrass theorem is used for continuous functions on
Rd. Among several variants, one simple statement is as follows:
[50]
- If ƒ : H → R is a convex continuous function such that ƒ(x) tends to +∞ when ||x|| tends to ∞, then ƒ admits a minimum at some point x0 ∈ H.
This fact (and its various generalizations) are fundamental for
direct methods in the
calculus of variations. Minimization results for convex functionals are also a direct consequence of the slightly more abstract fact that closed bounded convex subsets in a Hilbert space
H are
weakly compact, since
H is reflexive. The existence of weakly convergent subsequences is a special case of the
Eberlein-Šmulian theorem.
[edit] Banach space properties
Any general property of Banach spaces continues to hold for Hilbert spaces. The
open mapping theorem states that a
continuous surjective linear transformation from one Banach space to another is an
open mapping meaning that it sends open sets to open sets. A corollary is the
bounded inverse theorem, that a continuous and
bijective linear function from one Banach space to another is an isomorphism (that is, a continuous linear map whose inverse is also continuous). This theorem is considerably simpler to prove in the case of Hilbert spaces than in general Banach spaces.
[51] The open mapping theorem is equivalent to the
closed graph theorem, which asserts that a function from one Banach space to another is continuous if and only if its graph is a
closed set.
[52] In the case of Hilbert spaces, this is basic in the study of
unbounded operators (see
closed operator).
The (geometrical)
Hahn–Banach theorem asserts that a closed convex set can be separated from any point outside it by means of a
hyperplane of the Hilbert space. This is an immediate consequence of the
best approximation property: if
y is the element of a closed convex set
F closest to
x, then the separating hyperplane is the plane perpendicular to the segment
xy passing through its midpoint.
[53]
[edit] Operators on Hilbert spaces
[edit] Bounded operators
The
continuous linear operators A :
H1 →
H2 from a Hilbert space
H1 to a second Hilbert space
H2 are
bounded in the sense that they map
bounded sets to bounded sets. Conversely, if an operator is bounded, then it is continuous. The space of such
bounded linear operators has a
norm, the
operator norm given by

The sum and the composite of two bounded linear operators is again bounded and linear. For
y in
H2, the map that sends
x ∈
H1 to <
Ax,
y> is linear and continuous, and according to the Riesz representation theorem can therefore be represented in the form

for some vector
A∗y in
H1. This defines another bounded linear operator
A∗ :
H2 →
H1, the
adjoint of
A. One can see that
A∗∗ = A.
The set B(
H) of all bounded linear operators on
H, together with the addition and composition operations, the norm and the adjoint operation, is a
C*-algebra, which is a type of
operator algebra.
An element
A of B(
H) is called
self-adjoint or
Hermitian if
A∗ =
A. If
A is Hermitian and
〈Ax, x〉 ≥ 0 for every
x, then
A is called
non-negative, written
A ≥ 0; if equality holds only when
x = 0, then
A is called
positive. The set of self adjoint operators admits a
partial order, in which
A ≥
B if
A −
B ≥ 0. If
A has the form
B∗B for some
B, then
A is non-negative; if
B is invertible, then
A is positive. A converse is also true in the sense that, for a non-negative operator
A, there exists a unique non-negative
square root B such that

In a sense made precise by the
spectral theorem, self-adjoint operators can usefully be thought of as operators that are "real". An element
A of B(
H) is called
normal if
A∗A =
A A∗. Normal operators decompose into the sum of a self-adjoint operators and an imaginary multiple of a self adjoint operator
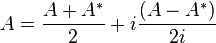
that commute with each other. Normal operators can also usefully be thought of in terms of their real and imaginary parts.
An element
U of B(
H) is called
unitary if
U is invertible and its inverse is given by
U∗. This can also be expressed by requiring that
U be onto
and〈Ux, Uy〉 =〈x, y〉 for all
x and
y in
H. The unitary operators form a
group under composition, which is the
isometry group of
H.
An element of B(
H) is
compact if it sends bounded sets to
relatively compact sets. Equivalently, a bounded operator
T is compact if, for any bounded sequence {
xk}, the sequence {
Txk} has a convergent subsequence. Many
integral operators are compact, and in fact define a special class of operators known as
Hilbert–Schmidt operators that are especially important in the study of
integral equations.
Fredholm operators are those which differ from a compact operator by a multiple of the identity, and are equivalently characterized as operators with a finite dimensional
kernel and
cokernel. The index of a Fredholm operator
T is defined by

The index is
homotopy invariant, and plays a deep role in
differential geometry via the
Atiyah–Singer index theorem.
[edit] Unbounded operators
Unbounded operators are also tractable in Hilbert spaces, and have important applications to
quantum mechanics.
[54] An unbounded operator
T on a Hilbert space
H is defined to be a linear operator whose domain
D(
T) is a linear subspace of
H. Often the domain
D(
T) is a dense subspace of
H, in which case
T is known as a
densely-defined operator.
The adjoint of a densely defined unbounded operator is defined in essentially the same manner as for bounded operators.
Self-adjoint unbounded operators play the role of the
observables in the mathematical formulation of quantum mechanics. Examples of self-adjoint unbounded operators on the Hilbert space
L2(
R) are:
[55]
- A suitable extension of the differential operator
-

- where i is the imaginary unit and f is a differentiable function of compact support.
- The multiplication-by-x operator:
-

These correspond to the
momentum and
position observables, respectively. Note that neither
A nor
B is defined on all of
H, since in the case of
A the derivative need not exist, and in the case of
B the product function need not be square integrable. In both cases, the set of possible arguments form dense subspaces of
L2(
R).
[edit] Constructions
[edit] Direct sums
Two Hilbert spaces
H1 and
H2 can be combined into another Hilbert space, called the
(orthogonal) direct sum,
[56] and denoted

consisting of the set of all
ordered pairs (
x1,
x2) where
xi ∈ Hi,
i = 1,2, and inner product defined by

More generally, if
Hi is a family of Hilbert spaces indexed by
i ∈ I, then the direct sum of the
Hi, denoted

consists of the set of all indexed families

in the
Cartesian product of the
Hi such that
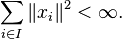
The inner product is defined by

Each of the
Hi is included as a closed subspace in the direct sum of all of the
Hi. Moreover, the
Hi are pairwise orthogonal. Conversely, if there is a system of closed subspaces
Vi,
i ∈ I, in a Hilbert space
H which are pairwise orthogonal and whose union is dense in
H, then
H is canonically isomorphic to the direct sum of
Vi. In this case,
H is called the internal direct sum of the
Vi. A direct sum (internal or external) is also equipped with a family of orthogonal projections
Ei onto the
ith direct summand
Hi. These projections are bounded, self-adjoint,
idempotent operators which satisfy the orthogonality condition

The
spectral theorem for
compact self-adjoint operators on a Hilbert space
H states that
H splits into an orthogonal direct sum of the eigenspaces of an operator, and also gives an explicit decomposition of the operator as a sum of projections onto the eigenspaces. The direct sum of Hilbert spaces also appears in quantum mechanics as the
Fock space of a system containing a variable number of particles, where each Hilbert space in the direct sum corresponds to an additional
degree of freedom for the quantum mechanical system. In
representation theory, the
Peter-Weyl theorem guarantees that any
unitary representation of a
compact group on a Hilbert space splits as the direct sum of finite-dimensional representations.
[edit] Tensor products
If
H1 and
H2, then one defines an inner product on the (ordinary)
tensor product as follows. On
simple tensors, let

This formula then extends by
sesquilinearity to an inner product on
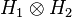
. The Hilbertian tensor product of
H1 and
H2, sometimes denoted by
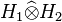
, is the Hilbert space obtained by completing
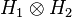
for the metric associated to this inner product.
[57]
An example is provided by the Hilbert space
L2([0, 1]). The Hilbertian tensor product of two copies of
L2([0, 1]) is isometrically and linearly isomorphic to the space
L2([0, 1]
2) of square-integrable functions on the square [0, 1]
2. This isomorphism sends a simple tensor

to the function

on the square.
This example is typical in the following sense.
[58] Associated to every simple tensor product
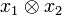
is the rank one operator

from the (continuous) dual
H1∗ to
H2. This mapping defined on simple tensors extends to a linear identification between
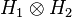
and the space of finite rank operators from
H1∗ to
H2. This extends to a linear isometry of the Hilbertian tensor product
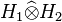
with the Hilbert space
HS(
H1∗,
H2) of
Hilbert-Schmidt operators from
H1∗ to
H2.
[edit] Orthonormal bases
The notion of an
orthonormal basis from linear algebra generalizes over to the case of Hilbert spaces.
[59] In a Hilbert space
H, an orthonormal basis is a family {
ek}
k ∈ B of elements of
H satisfying the conditions:
- Orthogonality: Every two different elements of B are orthogonal: 〈ek, ej〉= 0 for all k, j in B with k ≠ j.
- Normalization: Every element of the family has norm 1:||ek|| = 1 for all k in B.
- Completeness: The linear span of the family ek, k ∈ B, is dense in H.
A system of vectors satisfying the first two conditions basis is called an orthonormal system or an orthonormal set (or an orthonormal sequence if
B is
countable). Such a system is always
linearly independent. Completeness of an orthonormal system of vectors of a Hilbert space can be equivalently restated as:
- if 〈v, ek〉 = 0 for all k ∈ B and some v ∈ H then v = 0.
This is related to the fact that the only vector orthogonal to a dense linear subspace is the zero vector, for if
S is any orthonormal set and
v is orthogonal to
S, then
v is orthogonal to the closure of the linear span of
S, which is the whole space.
Examples of orthonormal bases include:
- the set {(1,0,0), (0,1,0), (0,0,1)} forms an orthonormal basis of R3 with the dot product;
- the sequence {ƒn : n ∈ Z} with ƒn(x) = exp(2πinx) forms an orthonormal basis of the complex space L2([0,1]);
In the infinite-dimensional case, an orthonormal basis will not be a basis in the sense of
linear algebra; to distinguish the two, the latter basis is also called a
Hamel basis. That the span of the basis vectors is dense implies that every vector in the space can be written as the sum of an infinite series, and the orthogonality implies that this decomposition is unique.
[edit] Sequence spaces
The space
ℓ 2 of square-summable sequences of complex numbers is the set of infinite sequences

of complex numbers such that

This space has an orthonormal basis:

More generally, if
B is any set, then one can form a Hilbert space of sequences with index set
B, defined by

The summation over
B is here defined by

the
supremum being taken over all finite subsets of
B. It follows that, in order for this sum to be finite, every element of
ℓ 2(
B) has only countably many nonzero terms. This space becomes a Hilbert space with the inner product

for all
x and
y in
ℓ 2(
B). Here the sum also has only countably many nonzero terms, and is unconditionally convergent by the Cauchy–Schwarz inequality.
An orthonormal basis of
ℓ 2(
B) is indexed by the set
B, given by

[edit] Bessel's inequality and Parseval's formula
Let
ƒ1, …, ƒn be a finite orthonormal system in
H. For an arbitrary vector
x in
H, let

Then
〈x, ƒk〉 =
〈y, ƒk〉 for every
k =
1, …, n. It follows that
x − y is orthogonal to each
ƒk, hence
x − y is orthogonal to
y. Using the Pythagorean identity twice, it follows that

Let
{ƒi }, i ∈ I, be an arbitrary orthonormal system in
H. Applying the preceding inequality to every finite subset
J of
I gives the
Bessel inequality[60]

(according to the definition of the
sum of an arbitrary family of non-negative real numbers).
Geometrically, Bessel's inequality implies that the orthogonal projection of
x onto the linear subspace spanned by the
fi has norm that does not exceed that of
x. In two dimensions, this is the assertion that the length of the leg of a right triangle may not exceed the length of the hypotenuse.
Bessel's inequality is a stepping stone to the more powerful
Parseval identity which governs the case when Bessel's inequality is actually an equality. If {
ek}
k ∈ B is an orthonormal basis of
H, then every element
x of
H may be written as

Even if
B is uncountable, Bessel's inequality guarantees that the expression is well-defined and consists only of countably many nonzero terms. This sum is called the
Fourier expansion of
x, and the individual coefficients 〈
x,
ek〉 are the
Fourier coefficients of
x. Parseval's formula is then

Conversely, if {
ek} is an orthonormal set such that Parseval's identity holds for every
x, then {
ek} is an orthonormal basis.
[edit] Hilbert dimension
As a consequence of
Zorn's lemma,
every Hilbert space admits an orthonormal basis; furthermore, any two orthonormal bases of the same space have the same
cardinality, called the Hilbert dimension of the space.
[61] For instance, since
ℓ2(
B) has an orthonormal basis indexed by
B, its Hilbert dimension is the cardinality of
B (which may be a finite integer, or a countable or uncountable
cardinal number).
As a consequence of Parseval's identity, if {
ek}
k ∈ B is an orthonormal basis of
H, then the map
Φ : H → ℓ
2(
B) defined by
Φ(x) = (〈x,ek〉)k∈B is an isometric isomorphism of Hilbert spaces: it is a bijective linear mapping such that

for all
x and
y in
H. The
cardinal number of
B is the Hilbert dimension of
H. Thus every Hilbert space is isometrically isomorphic to a sequence space ℓ
2(
B) for some set
B.
[edit] Separable spaces
A Hilbert space is
separable if and only if it admits a
countable orthonormal basis. All infinite-dimensional separable Hilbert spaces are therefore isometrically isomorphic to
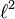
.
In the past, Hilbert spaces were often required to be separable as part of the definition.
[62] Most spaces used in physics are separable, and since these are all isomorphic to each other, one often refers to any infinite-dimensional separable Hilbert space as "
the Hilbert space" or just "Hilbert space".
[63] Even in
quantum field theory, most of the Hilbert spaces are in fact separable, as stipulated by the
Wightman axioms. However, it is sometimes argued that non-separable Hilbert spaces are also important in quantum field theory, roughly because the systems in the theory possess an infinite number of
degrees of freedom and any infinite Hilbert tensor product (of spaces of dimension greater than one) is non-separable.
[64] For instance, a
bosonic field can be naturally thought of as an element of a tensor product whose factors represent harmonic oscillators at each point of space. From this perspective, the natural state space of a boson might seem to be a non-separable space.
[64] However, it is only a small separable subspace of the full tensor product that can contain physically meaningful fields (on which the observables can be defined). Another non-separable Hilbert space models the state of an infinite collection of particles in an unbounded region of space. An orthonormal basis of the space is indexed by the density of the particles, a continuous parameter, and since the set of possible densities is uncountable, the basis is not countable.
[64]
[edit] Orthogonal complements and projections
If
S is a subset of a Hilbert space
H, the set of vectors orthogonal to
S is defined by

S⊥ is a
closed subspace of
H and so forms itself a Hilbert space. If
V is a closed subspace of
H, then
V⊥ is called the
orthogonal complement of
V. In fact, every
x in
H can then be written uniquely as
x =
v +
w, with
v in
V and
w in
V⊥. Therefore,
H is the internal Hilbert direct sum of
V and
V⊥.
The linear operator P
V :
H →
H which maps
x to
v is called the
orthogonal projection onto
V. There is a
natural one-to-one correspondence between the set of all closed subspaces of
H and the set of all bounded self-adjoint operators
P such that
P2 =
P. Specifically,
- Theorem. The orthogonal projection PV is a self-adjoint linear operator on H of norm ≤ 1 with the property P2V = PV. Moreover, any self-adjoint linear operator E such that E2 = E is of the form PV, where V is the range of E. For every x in H, PV(x) is the unique element v of V which minimizes the distance ||x − v||.
This provides the geometrical interpretation of P
V(
x): it is the best approximation to
x by elements of
V.
[65]
An operator
P such that
P =
P2 =
P∗ is called an orthogonal projection. The orthogonal projection
PV onto a closed subspace
V of
H is the adjoint of the
inclusion mapping

meaning that

for all
x ∈
H and
y ∈
V. Projections
PU and
PV are called mutually orthogonal if
PUPV = 0. This is equivalent to
U and
V being orthogonal as subspaces of
H. As a result, the sum of the two projections
PU and
PV is only a projection if
U and
V are orthogonal to each other, and in that case
PU +
PV =
PU+V. The composite
PUPV is generally not a projection; in fact, the composite is a projection if and only if the two projections commute, and in that case
PUPV =
PU∩V.
The operator norm of a projection
P onto a non-zero closed subspace is equal to one:

Every closed subspace
V of a Hilbert space is therefore the image of an operator
P of norm one such that
P2 =
P. In fact this property characterizes Hilbert spaces:
[66]
- A Banach space of dimension higher than 2 is (isometrically) a Hilbert space if and only if, to every closed subspace V, there is an operator PV of norm one whose image is V such that

While this result characterizes the metric structure of a Hilbert space, the structure of a Hilbert space as a
topological vector space can itself be characterized in terms of the presence of complementary subspaces:
[67]
- A Banach space X is topologically and linearly isomorphic to a Hilbert space if and only if, to every closed subspace V, there is a closed subspace W such that X is equal to the internal direct sum
 .
.
The orthogonal complement satisfies some more elementary results. It is a
monotone function in the sense that if
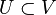
, then

with equality holding if and only if
V is contained in the
closure of
U. This result is a special case of the
Hahn–Banach theorem. The closure of a subspace can be completely characterized in terms of the orthogonal complement: If
V is a subspace of
H, then the closure of
V is equal to

. The orthogonal complement is thus a
Galois connection on the
partial order of subspaces of a Hilbert space. In general, the orthogonal complement of a sum of subspaces is the intersection of the orthogonal complements:
[68] 
. If the
Vi are in addition closed, then

.
[edit] Spectral theory
There is a well-developed
spectral theory for self-adjoint operators in a Hilbert space, that is roughly analogous to the study of
symmetric matrices over the reals or self-adjoint matrices over the complex numbers.
[69] In the same sense, one can obtain a "diagonalization" of a self-adjoint operator as a suitable sum (actually an integral) of orthogonal projection operators.
The
spectrum of an operator T, denoted σ(
T) is the set of complex numbers λ such that
T − λ lacks a continuous inverse. If
T is bounded, then the spectrum is always a
compact set in the complex plane, and lies inside the disc

If
T is self-adjoint, then the spectrum is real. In fact, it is contained in the interval [
m,
M] where

Moreover,
m and
M are both actually contained within the spectrum.
The eigenspaces of an operator
T are given by

Unlike with finite matrices, not every element of the spectrum of
T must be an eigenvalue: the linear operator
T − λ may only lack an inverse because it is not surjective. Elements of the spectrum of an operator in the general sense are known as
spectral values. Since spectral values need not be eigenvalues, the spectral decomposition is often more subtle than in finite dimensions.
However, the
spectral theorem of a self-adjoint operator
T takes a particularly simple form if, in addition,
T is assumed to be a
compact operator. The
spectral theorem for compact self-adjoint operators states:
[70]
- A compact self-adjoint operator T has only countably (or finitely) many spectral values. The spectrum of T has no limit point in the complex plane except possibly zero. The eigenspaces of T decompose H into an orthogonal direct sum:

- Moreover, if Eλ denotes the orthogonal projection onto the eigenspace Hλ, then

- where the sum converges with respect to the norm on B(H).
This theorem plays a fundamental role in the theory of
integral equations, as many integral operators are compact, in particular those that arise from
Hilbert-Schmidt operators.
The general spectral theorem for self-adjoint operators involves a kind of operator-valued
Riemann–Stieltjes integral, rather than an infinite summation.
[71] The
spectral family associated to
T associates to each real number λ an operator
Eλ, which is the projection onto the nullspace of the operator
(T − λ) + , where the positive part of a self-adjoint operator is defined by

The operators
Eλ are monotone increasing relative to the partial order defined on self-adjoint operators; the eigenvalues correspond precisely to the jump discontinuities. One has the spectral theorem, which asserts

The integral is understood as a Riemann–Stieltjes integral, convergent with respect to the norm on B(
H). In particular, one has the ordinary scalar-valued integral representation

A somewhat similar spectral decomposition holds for normal operators, although because the spectrum may now contain non-real complex numbers, the operator-valued Stieltjes measure
dEλ must instead be replaced by a
resolution of the identity.
A major application of spectral methods is the
spectral mapping theorem, which allows one to apply to a self-adjoint operator
T any continuous complex function
ƒ defined on the spectrum of
T by forming the integral

The resulting
continuous functional calculus has applications in particular to
pseudodifferential operators.
[72]
The spectral theory of
unbounded self-adjoint operators is only marginally more difficult than for bounded operators. The spectrum of an unbounded operator is defined in precisely the same way as for bounded operators: λ is a spectral value if the
resolvent operator
- Rλ = (T − λ) − 1
fails to be a well-defined continuous operator. The self-adjointness of
T still guarantees that the spectrum is real. Thus the essential idea of working with unbounded operators is to look instead at the resolvent
Rλ where λ is non-real. This is a
bounded normal operator, which admits a spectral representation that can then be transferred to a spectral representation of
T itself. A similar strategy is used, for instance, to study the spectrum of the Laplace operator: rather than address the operator directly, one instead looks as an associated resolvent such as a
Riesz potential or
Bessel potential.
A precise version of the spectral theorem which holds in this case is:
[73]
- Given a densely-defined self-adjoint operator T on a Hilbert space H, there corresponds a unique resolution of the identity E on the Borel sets of R, such that

- for all x ∈ D(T) and y ∈ H. The spectral measure E is concentrated on the spectrum of T.
There is also a version of the spectral theorem that applies to unbounded normal operators.
literally copied from : http://en.wikipedia.org/wiki/Hilbert_space






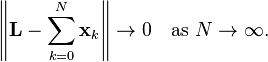









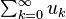




















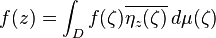



![-\frac{d}{dx}\left[p(x)\frac{dy}{ dx}\right]+q(x)y=\lambda w(x)y](http://upload.wikimedia.org/math/4/6/8/46843bd5250780c5b80f9ce7cedb4a94.png)
















 = 0. The notation for this is
= 0. The notation for this is 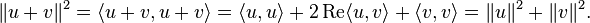




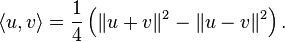




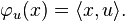
 is an antilinear mapping from H to H∗. The Riesz representation theorem states that this mapping is an antilinear isomorphism.
is an antilinear mapping from H to H∗. The Riesz representation theorem states that this mapping is an antilinear isomorphism.

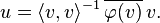





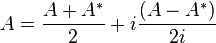







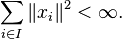



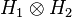 . The Hilbertian tensor product of H1 and H2, sometimes denoted by
. The Hilbertian tensor product of H1 and H2, sometimes denoted by 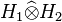 , is the Hilbert space obtained by completing
, is the Hilbert space obtained by completing  to the function
to the function
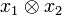 is the rank one operator
is the rank one operator













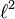 .
.




 .
.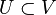 , then
, then  with equality holding if and only if V is contained in the
with equality holding if and only if V is contained in the  . The orthogonal complement is thus a
. The orthogonal complement is thus a  . If the Vi are in addition closed, then
. If the Vi are in addition closed, then  .
. If T is self-adjoint, then the spectrum is real. In fact, it is contained in the interval [m,M] where
If T is self-adjoint, then the spectrum is real. In fact, it is contained in the interval [m,M] where







